ID: 19393

传统题

1000ms

128MiB

尝试: 3

已通过: 6

难度: 10

上传者:

tobyforever

笑话：

有一天阿东到图书馆借了 N 本书，出图书馆的时候，警报响了，于是保安把阿东拦下，要检查一下哪本书没有登记出借。阿东正准备把每一本书在报警器下过一下，以找出引发警报的书，但是保安露出不屑的眼神：你连二分查找都不会吗？

于是保安把书分成两堆，让第一堆过一下报警器，报警器响，这说明引起报警的书包含在里面；于是再把这堆书分成两堆，把第一堆过一下报警器，报警器又响，继续分成两堆……

最终，检测了 logN 次之后，保安成功的找到了那本引起警报的书，露出了得意和嘲讽的笑容。于是阿东背着剩下的书走了。

从此，图书馆丢了 N - 1 本书（手动狗头）。

解释：

这是一个非常经典的程序员式冷笑话，它结合了算法效率、逻辑盲点与现实世界的反差。作为一名教练，我分三个层次为你拆解这个笑话的精髓：

1. 算法层： $O(N)$ vs $O(\log N)$ 的降维打击

阿东的思路（线性查找）：一本书一本书地过报警器。如果借了 $N$ 本书，最坏情况下要试 $N$ 次。时间复杂度是 $O(N)$ 。
保安的思路（二分查找）：把书分成两半，只测其中一半。如果响了，目标就在这半堆；如果不响，目标就在另一半。每次排除一半，时间复杂度是 $O(\log N)$ 。
笑点所在：保安表现出一种“技术优越感”，嘲讽阿东不懂计算机科学中最基础的优化算法。在 $N=1024$ 时，阿东要试 1024 次，而保安只需 10 次。

2. 逻辑层：二分查找的“前提条件”

这个笑话最硬核的逻辑点在于：二分查找只能在“只有一个目标”或者“寻找任一目标”的情况下完美工作。

报警器的逻辑：报警器响，意味着“这堆书里至少有一本没登记”。
保安的错误假设：保安默认“只有一本书”没登记。
二分法的盲区：
- 如果阿东其实 $N$ 本书全都没登记呢？
- 保安把书分成 A、B 两堆。测 A 堆，报警器响了（因为 A 堆里有没登记的书）。
- 保安于是理所当然地认为“那看来问题出在 A 堆”，于是把 B 堆扔在一边不管了。
- 实际上，B 堆里全是偷来的书，但因为保安只关注排除出来的“那一本”，导致其他所有没登记的书都成了漏网之鱼。

3. 结局层：书是怎么丢的？（神转折）

最终结果：保安通过精密的 $\log N$ 次检测，确实抓到了那一本“没登记的书”。他觉得自己效率极高，不仅抓到了“贼”，还省了时间。
现实反转：阿东其实借了 $N$ 本书，每一本都没登记。保安帮他找出了其中一本，剩下的 $N-1$ 本，保安以为是“经过检测没问题”的，直接放行了。
讽刺点：保安赢了算法，输了业务。他自诩懂算法，却忘了安保工作的本质不是“寻找一个异常”，而是“排除所有异常”。

教练总结

这题的关键词是：单一目标假设。

在 NOI 竞赛中，我们也经常提醒选手：

二分法虽然快，但一定要注意单调性和判定条件的准确性。
不要为了追求时间复杂度的极致优化，而忽略了逻辑覆盖的完整性（比如这题，保安漏掉了对另一半区间的校验）。

这个笑话告诉我们： 算法再好，如果底层逻辑（业务需求）理解错了，优化得越快，损失就越大！

为什么二分查找算法看上去简单，实际上有很多细节陷阱？

你好！我是你的 NOI 竞赛教练。

刚才你分享的那个关于阿东和保安的笑话，其实是理解二分查找“细节陷阱”的绝佳切入点。很多同学觉得二分查找简单，是因为它的核心思想（折半）只要 10 秒就能听懂；但真正写对它很难，是因为边界条件（Boundary Conditions）和搜索区间（Search Interval）的逻辑严密性要求极高。

下面我为你总结labuladong讲二分查找里的核心框架，并以启发式的方法带你拆解这些“磨人的细节”。

一、 Labuladong 二分查找框架总结

框架的核心思想是：“统一认知，消除歧义”。

1. 基本模板：寻找一个数

搜索区间：[left, right] （闭区间）。
循环条件：while (left <= right)。因为区间是闭的，当 left == right 时，区间内还有一个数没看，所以要继续。
更新逻辑：发现 nums[mid] 不是目标，去 [left, mid-1] 或 [mid+1, right] 找。

2. 左侧边界搜索：寻找第一个出现的 target

核心逻辑：找到 target 时不要停！缩小右边界 right = mid - 1，并在 mid 左侧继续寻找，试图把“包围圈”往左赶。
越界检查：最后要检查 left 是否出界以及 nums[left] 是否真的等于 target。

3. 右侧边界搜索：寻找最后一个出现的 target

核心逻辑：找到 target 时不要停！缩小左边界 left = mid + 1，并在 mid 右侧继续寻找。
越界检查：最后要检查 right 是否出界以及 nums[right] 是否等于 target。

二、启发式讲解：为什么二分查找容易写错？

二分查找之所以是“细节狂魔”，是因为它涉及到了计算机科学中最微小但也最致命的错误：Off-by-one error（差一错误）。

请跟我一起在草稿纸上完成以下三个思维实验：

1. 思维实验一：你定义的“盒子”长什么样？

想象你面前有一排盒子。二分查找就是在缩窄范围。

如果你定义范围是“从第 left 到第 right 个盒子（包含 right）”，这就是 闭区间 [left, right]。
如果你定义范围是“从第 left 到第 right 个，但不包含第 right 个”，这就是 左闭右开 [left, right)。

易错点提示： 很多同学在初始化时写 right = n - 1（闭区间），但在循环时写 while (left < right)（开区间条件）。

结果：当 left == right 时，你的程序以为“盒子缩没了”，其实里面还剩一个盒子没拆开看！这就是丢失数据的开始。

2. 思维实验二：当“相等”发生时，你在想什么？

这就是那个“图书馆保安”笑话的精髓。

保安的问题：一发现响声（匹配），就认为找到了唯一目标，扔掉了另一半。
正确思维：如果你要找的是第一个没登记的书。
- 当 mid 位置的书报警时，它可能是第一个，但也可能它左边还有没登记的书。
- 所以，你不能停，你要把 right 挪到 mid - 1，继续看左边那一堆。

3. 思维实验三：程序停止的一瞬间，指针在哪里？

这是二分查找最难推理的地方。

在 while (left <= right) 且没有找到目标时，循环结束的那一刻，一定满足 left = right + 1。
这意味着什么？这意味着 left 指向的是第一个大于 target 的位置（即拟插入位置）。

三、教练的避坑总结：三看原则

在 NOI 考场上，写完二分查找后，请务必进行这三次心理审查：

一看初始化与条件是否匹配：
- 初始化 right = n - 1 $\rightarrow$ 必须配 while (left <= right)。
- 初始化 right = n $\rightarrow$ 必须配 while (left < right)。
- 理由：确保每一个可能的元素都进入了搜索视野。
二看 mid 的更新是否会导致死循环：
- 是否总是 left = mid + 1 或 right = mid - 1？
- 如果写成了 left = mid，当 left 和 right 相邻时（例如 left=0, right=1），mid 永远等于 0，left 永远不更新，程序就卡死了。
三看返回值的越界检查：
- 搜左侧边界时，如果 target 比所有数都大，left 会一直加到 n。
- 直接访问 nums[left] 会导致 Runtime Error。

四、时间与空间复杂度分析

时间复杂度：始终为 $O(\log N)$ $O (lo g N)$ 。因为每次问题的规模都减半。
- 优化建议：计算 mid 时，不要写 (left + right) / 2，容易因溢出报错。请写 left + (right - left) / 2。
空间复杂度：迭代写法为 $O(1)$ ，递归写法为 $O(\log N)$ （占用栈空间）。在竞赛中，强烈建议使用迭代写法。

总结一句话：二分查找的逻辑不是在代码里，而是在你对**“搜索区间”定义的严死合缝**的坚持里。只要你定义了区间是闭的，那么后续所有 +1、-1 和循环判断，都必须为这个“闭”服务。

那个保安之所以丢了书，就是因为他在“响了”之后，没能维持正确的搜索区间逻辑！

总结表格

你好！作为教练，我深知在紧张的考场上，模糊的逻辑是致错的根源。为了让你彻底告别“二分玄学”，我将 闭区间 [left, right] 这一最稳健的写法总结为下表。

掌握这个表格的核心在于理解：当 while (left <= right) 终止时，left = right + 1，此时搜索区间刚好被“耗尽”。

二分查找核心情形对比总结表

查找情形	查找目标	搜索区间与循环条件	`nums[mid] == target` 时	指针更新逻辑	最终返回与越界检查	原理记忆法 (核心思想)
基础查找	寻找目标值，找到即返回	`L = 0, R = n-1` `while (L <= R)`	立即返回 `mid`	`L = mid + 1` `R = mid - 1`	返回 `-1` (未找到)	“见好就收”：找到就撤，两边收缩。
左侧边界	寻找第一个出现的 `target`		收缩右界： `R = mid - 1`		返回 `L`。检查 `L >= n` 或 `nums[L] != target`	“左侧贪婪”：即使相等也要向左挤，压缩 `R`。
右侧边界	寻找最后一个出现的 `target`		收缩左界： `L = mid + 1`		返回 `R`。检查 `R < 0` 或 `nums[R] != target`	“右侧贪婪”：即使相等也要向右挤，压缩 `L`。

启发式原理记忆法：为什么这样写？

为了让你在草稿纸上能瞬间推演出来，请记住这三条“金律”：

1. 区间定义神圣不可侵犯（The Sacred Interval）

如果我们定义区间是 [left, right]，那么 left = 0, right = n - 1。
既然是闭区间，while (left <= right) 的终止条件就是 left == right + 1，此时区间变为了 [right + 1, right]，刚好为空，逻辑完美自洽。
注意：所有 mid 已经检查过不是目标，所以必须 +1 或 -1 跳过 mid。

2. “保安逻辑”与“贪婪收缩”（The Greedy Shrink）

寻找左侧边界：当你发现 nums[mid] == target 时，你就像那个保安一样，虽然抓到了一个，但你怀疑左边还有“没登记的书”。所以你坚决地把右边界 R 挪到 mid - 1。
结果：R 会不断把 L 往左边推，直到 L 停在第一个 target 的位置。

3. 终止后的“错位”状态（Post-Loop State）

循环结束时，L 和 R 的关系是：R | L。
左侧查找：由于 R 一直在往左收缩，最后 L 会落在第一个 target 上，而 R 落在它的左邻居上。
右侧查找：由于 L 一直在往右收缩，最后 R 会落在最后一个 target 上，而 L 落在它的右邻居上。

NOI 考场避坑建议 (Tips for Pro)

防止溢出：
- 不要写 mid = (L + R) / 2;
- 要写 mid = L + (R - L) / 2; (这是 NOI 选手的基本修养)。
强制检查越界：
- 二分结束后，L 可能等于 n（target 太大），R 可能等于 -1（target 太小）。
- 必须先判断索引是否合法，再访问 nums[idx]。
时间复杂度优化：
- 二分查找是 $O(\log N)$ 。
- 如果是在 std::set 或 std::map 中查找，请使用 container.lower_bound() 成员函数，不要使用全局 std::lower_bound，否则复杂度会退化为 $O(N)$ （因为迭代器不是随机访问的）。

一句话总结记忆：

闭区间，等号连；左边界，改右端；右边界，改左边；结束之后看一眼（防越界）。

STL的lower_bound和upper_bound和上面知识点有什么关系？

你好！我是你的 OI 教练。在竞赛中，熟练使用 STL 的 lower_bound 和 upper_bound 是基本功，但如果不理解它们与前面讲到的“二分查找框架”的关系，很容易在处理边界问题时丢分。

我们将 STL 函数与之前的“左边界”、“右边界”知识点进行深度映射：

一、核心定义映射

STL 的设计基于 左闭右开区间 [first, last)，其返回的是一个迭代器（指针）。

STL 函数	逻辑定义	对应框架知识点	查找目标（形象理解）
`lower_bound`	返回第一个 $\ge$ target 的位置	左侧边界查找	寻找 target 的“起始阵地”
`upper_bound`	返回第一个 $>$ target 的位置	右侧边界的“邻居”	寻找 target 阵地的“后方出口”

二、启发式对比：STL 逻辑 vs 闭区间框架

我们在草稿纸上对比一下 STL 的实现逻辑和你之前掌握的闭区间逻辑：

1. `lower_bound` 逻辑（寻找第一个 $\ge$ target）

它其实就是我们说的左侧边界查找。

如果 target 存在，它指向第一个 target。
如果 target 不存在，它指向第一个比 target 大的数（即 target 应该插入的位置）。
记忆点：它是最常用的，用来确定一个数“至少”该从哪开始出现。

2. `upper_bound` 逻辑（寻找第一个 $>$ target）

它相当于右侧边界查找的后一个位置。

即使 target 存在，它也绝不返回 target 的位置，而是返回 target 阵地后面的那个“外人”。
记忆点：它和 lower_bound 配合，刚好形成一个左闭右开区间 [lower_bound, upper_bound)，这个区间里全是 target。

三、竞赛常用“魔法公式”

在 NOI 考场上，我们经常需要实现更具体的功能。利用 STL 函数，你可以直接写出以下逻辑：

查找第一个等于 target 的位置：

auto it = lower_bound(v.begin(), v.end(), target);
if (it != v.end() && *it == target) 
    return distance(v.begin(), it);
else 
    return -1; // 不存在

查找最后一个等于 target 的位置：
```
auto it = upper_bound(v.begin(), v.end(), target);
if (it != v.begin() && *prev(it) == target) 
    return distance(v.begin(), prev(it));
else 
    return -1;
```
启发思维：为什么是 prev(it)？因为 upper_bound 找的是第一个“大过头”的数，那它左边那个数（如果存在）才可能是我们要找的“最后一个 target”。

统计 target 出现的次数：

int count = upper_bound(v.begin(), v.end(), target) - lower_bound(v.begin(), v.end(), target);

四、教练的特别警告（NOI 避坑必看）

1. 容器陷阱（性能致命伤）

这是很多 OI 选手从“省一”跌到“省二”的原因：

错误写法：std::lower_bound(s.begin(), s.end(), x) —— 如果 s 是 std::set 或 std::map。
- 后果：复杂度退化为 $O(N)$ ！因为 set 的迭代器不是随机访问迭代器，std::lower_bound 只能跳着走，但每一步都要模拟二分，导致效率极低。
正确写法：s.lower_bound(x) —— 使用容器自带的成员函数。
- 后果：标准的 $O(\log N)$ 。

2. 这里的“二分”不是万能的

STL 函数要求序列必须是 有序（Sorted） 或者 已划分（Partitioned） 的。

如果序列无序，lower_bound 不会报错，但会返回一个毫无意义的错误结果。

3. 结构体与自定义比较

如果要在自定义结构体 struct Node 上使用 lower_bound，必须：

重载 < 运算符。
或者在调用时传入自定义比较函数 cmp。
注意：lower_bound 内部只使用 < 比较，它判断 a == b 的逻辑是 !(a < b) && !(b < a)。

五、总结图示

假设数组为：[1, 2, 2, 2, 3, 5]，查找 target = 2：

数值:   1    2    2    2    3    5
索引:   0    1    2    3    4    5
            ^              ^
            |              |
      lower_bound     upper_bound
      (第一个 >= 2)    (第一个 > 2)

教练总结： STL 的这两个函数本质上是帮你处理好了所有二分边界细节的“黑盒子”。理解了前面的框架，你就能明白为什么 upper_bound - lower_bound 能算个数，也能明白为什么在找不到 target 时，它们会指向同一个位置。

在考场上，能用 STL 就用 STL，因为它们的边界逻辑是经过千万次测试的，比现场手写更安全！但如果是做“二分答案”类题目，你还是得手写框架。加油！

二分查找模板题

你好！作为一名 OI 教练，我为你准备了一道最经典的二分查找全能模板题。这道题不仅要求你找到目标，还要求你精确锁定目标在重复序列中的起始和终止位置，这完美涵盖了二分查找的所有边界情况。

一、预备知识点

单调性：二分查找的前提是序列必须有序（递增或递减）。
区间闭合性：统一使用 [left, right] 闭区间逻辑。
查找边界：
- 左边界：第一个 $\ge$ 目标值的位置。
- 右边界：最后一个 $\le$ 目标值的位置。

二、题目描述 (NOI 风格)

题目名称：数目的范围 (Range of Numbers) 时间限制：1.0s 内存限制：256MB

【问题描述】 给定一个长度为 $n$ 的非减（从小到大）整数数列，以及 $m$ 个查询。对于每个查询 $k$ ，请输出 $k$ 在数列中出现的起始编号和终止编号（从 $0$ 开始编号）。如果数列中不存在该数，则输出 -1 -1。

【输入格式】 第一行包含两个整数 $n$ 和 $m$ ，分别表示数列长度和查询次数。第二行包含 $n$ 个整数，表示数列本身。接下来 $m$ 行，每行包含一个整数 $k$ ，表示一个查询。

【输出格式】 共 $m$ 行，每行包含两个整数，表示起始编号和终止编号。

【样例输入】

6 3
1 2 2 2 3 4
2
3
5

【样例输出】

1 3
4 4
-1 -1

【数据范围说明】

$1 \le n \le 100,000$
$1 \le m \le 10,000$
数列中的值及查询值均在 $[1, 10^9]$ 范围内。

三、教学启发与草稿纸推演

让我们在草稿纸上模拟查询 target = 2 的过程，数列为 1 2 2 2 3 4。

1. 寻找左边界 (第一个 2)

初值：L = 0, R = 5, mid = 2。
nums(2) 是 2，虽然找到了，但不满足。我们要找最左边的，所以认为右边都没用了，强制收缩右界：R = mid - 1 = 1。
结论：当 nums(mid) >= target 时，我们要不断压迫 R 向左走。最终 L 会停在第一个 2 的位置。

2. 寻找右边界 (最后一个 2)

初值：L = 0, R = 5, mid = 2。
nums(2) 是 2，不满足。我们要找最右边的，所以强制收缩左界：L = mid + 1 = 3。
结论：当 nums(mid) <= target 时，我们要不断压迫 L 向右走。最终 R 会停在最后一个 2 的位置。

3. 复杂度与优化

时间： $M$ 次查询，每次 $O(\log N)$ 。总复杂度 $O(M \log N)$ 。对于 $10^5$ 级数据，单次查询只需 17 次左右比对。
空间： $O(N)$ 存储数组。

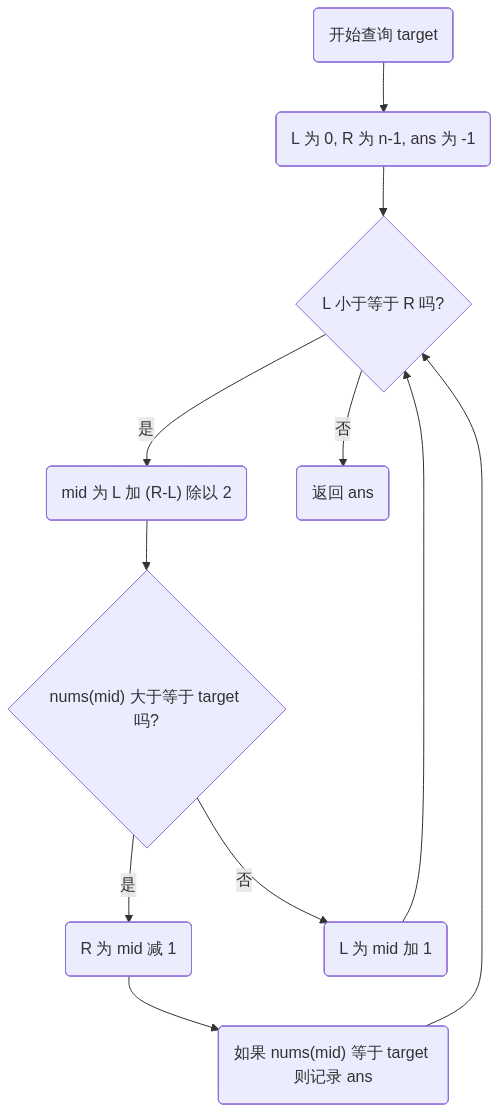
四、算法流程图 (左边界查找示例)

graph TD
    Start("开始查询 target") --> Init("L 为 0, R 为 n-1, ans 为 -1")
    Init --> WhileCond{"L 小于等于 R 吗?"}
    
    WhileCond -- "是" --> CalcMid("mid 为 L 加 (R-L) 除以 2")
    CalcMid --> Compare{"nums(mid) 大于等于 target 吗?"}
    
    Compare -- "是" --> MoveR("R 为 mid 减 1")
    MoveR --> SavePos("如果 nums(mid) 等于 target 则记录 ans")
    
    Compare -- "否" --> MoveL("L 为 mid 加 1")
    
    SavePos --> WhileCond
    MoveL --> WhileCond
    
    WhileCond -- "否" --> End("返回 ans")

五、 NOI 竞赛级伪代码提示 (C++14)

// 查找第一个大于等于 x 的位置
int find_first(int x) {
    int l = 0, r = n - 1, res = -1;
    while (l <= r) {
        int mid = l + (r - l) / 2;
        if (a[mid] >= x) {
            if (a[mid] == x) res = mid; // 记录候选答案
            r = mid - 1; // 尝试在左半部分找更早的
        } else {
            l = mid + 1;
        }
    }
    return res;
}

// 查找最后一个小于等于 x 的位置
int find_last(int x) {
    int l = 0, r = n - 1, res = -1;
    while (l <= r) {
        int mid = l + (r - l) / 2;
        if (a[mid] <= x) {
            if (a[mid] == x) res = mid; // 记录候选答案
            l = mid + 1; // 尝试在右半部分找更晚的
        } else {
            r = mid - 1;
        }
    }
    return res;
}

六、关键词理解 (读题技巧)

“从小到大/有序”：这是二分查找到灵魂。如果没有这几个字，必须先 $O(N \log N)$ 排序。
“第一个/起始”：提示使用左侧边界二分。
“最后一个/终止”：提示使用右侧边界二分。
“不存在输出 -1”：提示在二分函数中，初始化结果为 -1，且只有在 nums(mid) == target 时才更新结果。

优化建议：在处理 $10^5$ 以上的查询时，请务必使用 scanf/printf 或关闭流同步的 cin/cout，否则 IO 可能会成为性能瓶颈。同时，计算 mid 时使用 l + (r - l) / 2 可以防止 l + r 溢出 int 的最大范围。加油！

#19393. 二分查找思想框架和模板

二分查找思想框架和模板

笑话：

解释：

1. 算法层：O(N)O(N)O(N) vs O(log⁡N)O(\log N)O(logN) 的降维打击