这是一个非常适合初学者理解哈希表底层原理的精简版代码。

特点：

1. 结构清晰：使用“数组+链表”的标准拉链法结构。
2. 逻辑直观：去掉了复杂的模板和迭代器，使用最基础的指针操作。
3. 核心完整：完整包含了哈希计算、冲突处理、节点查找、删除以及核心难点——动态扩容 (Rehash)。

/**
 * 题目：手写 HashMap 实现原理 (精简教学版)
 * 语言：C++14
 */
#include <iostream>
#include <vector>
#include <string>

using namespace std;

// 1. 定义链表节点：用于解决哈希冲突 (拉链法)
struct Node {
    int key;
    int val;
    Node* next; // 指向下一个节点
    
    // 构造函数：方便创建新节点
    Node(int k, int v, Node* n) : key(k), val(v), next(n) {}
};

// 全局变量模拟哈希表
vector<Node*> buckets; // 桶数组 (存放链表头指针)
int capacity = 16;     // 初始容量
int num_elements = 0;  // 当前元素个数

// 2. 扩容函数 (Rehash) - 核心难点
void resize() {
    int old_cap = capacity;
    capacity *= 2; // 容量翻倍
    
    // 保存旧桶，创建新桶
    vector<Node*> old_buckets = buckets;
    buckets.assign(capacity, nullptr); // 重置并扩大桶数组，初始化为空
    
    // 遍历旧桶中的所有节点，搬家到新桶
    for (int i = 0; i < old_cap; i++) {
        Node* curr = old_buckets[i];
        while (curr != nullptr) {
            Node* next_node = curr->next; // 先记录下一个节点，防止断链
            
            // 重新计算哈希值 (因为 capacity 变了)
            int new_idx = curr->key % capacity;
            
            // 头插法搬入新家
            curr->next = buckets[new_idx];
            buckets[new_idx] = curr;
            
            curr = next_node; // 继续处理旧链表的下一个
        }
    }
}

// 3. 插入/更新操作 (Put)
void put(int key, int val) {
    int idx = key % capacity;
    Node* curr = buckets[idx];
    
    // 遍历链表，看 key 是否已存在
    while (curr != nullptr) {
        if (curr->key == key) {
            curr->val = val; // 存在则更新值
            return;
        }
        curr = curr->next;
    }
    
    // 不存在，创建新节点并使用"头插法"插入
    buckets[idx] = new Node(key, val, buckets[idx]);
    num_elements++;
    
    // 检查负载因子：如果 元素数量 > 容量 * 0.75，则扩容
    if (num_elements * 1.0 / capacity > 0.75) {
        resize();
    }
}

// 4. 查询操作 (Get)
int get(int key) {
    int idx = key % capacity;
    Node* curr = buckets[idx];
    
    while (curr != nullptr) {
        if (curr->key == key) {
            return curr->val; // 找到返回 value
        }
        curr = curr->next;
    }
    return -1; // 没找到
}

// 5. 删除操作 (Remove)
void remove(int key) {
    int idx = key % capacity;
    Node* curr = buckets[idx];
    Node* prev = nullptr; // 记录前驱节点
    
    while (curr != nullptr) {
        if (curr->key == key) {
            // 找到了，准备删除
            if (prev == nullptr) {
                // 删除的是头节点
                buckets[idx] = curr->next;
            } else {
                // 删除的是中间节点
                prev->next = curr->next;
            }
            delete curr; // 释放内存
            num_elements--;
            return;
        }
        prev = curr;
        curr = curr->next;
    }
}

int main() {
    // 优化 I/O 速度
    ios::sync_with_stdio(false);
    cin.tie(nullptr);

    // 初始化桶数组
    buckets.assign(capacity, nullptr);

    int N;
    cin >> N;
    
    while (N--) {
        string op;
        cin >> op;
        
        int x, y;
        if (op == "put") {
            cin >> x >> y;
            put(x, y);
        } else if (op == "get") {
            cin >> x;
            cout << get(x) << "\n";
        } else if (op == "remove") {
            cin >> x;
            remove(x);
        }
    }
    
    return 0;
}

👨‍💻 初学者学习重点 (代码解析)

1. 数据结构 (vector<Node*> buckets)：

   • 想象一个大柜子（Vector），里面有很多抽屉。
   • 每个抽屉里不直接放东西，而是放一根绳子（指针），绳子上串着很多卡片（Linked List）。
   • 这就是“拉链法”：key % capacity 算出抽屉编号，如果冲突了，就串在同一个抽屉的绳子上。

2. 头插法 (buckets[idx] = new Node(..., buckets[idx]))：

   • 这是插入链表最快的方式。不管链表有多长，新来的直接做“老大”（排在第一个），把原来的老大接在自己后面。
   • 复杂度永远是 $O(1)$。

3. 扩容 (resize) 的必要性：

   • 如果不扩容，随着数据越来越多，绳子（链表）会越来越长，查找就变成了遍历长链表，速度变慢。
   • 扩容就是“买个更大的柜子”，把旧卡片重新算位置放进去，保证每根绳子都很短。

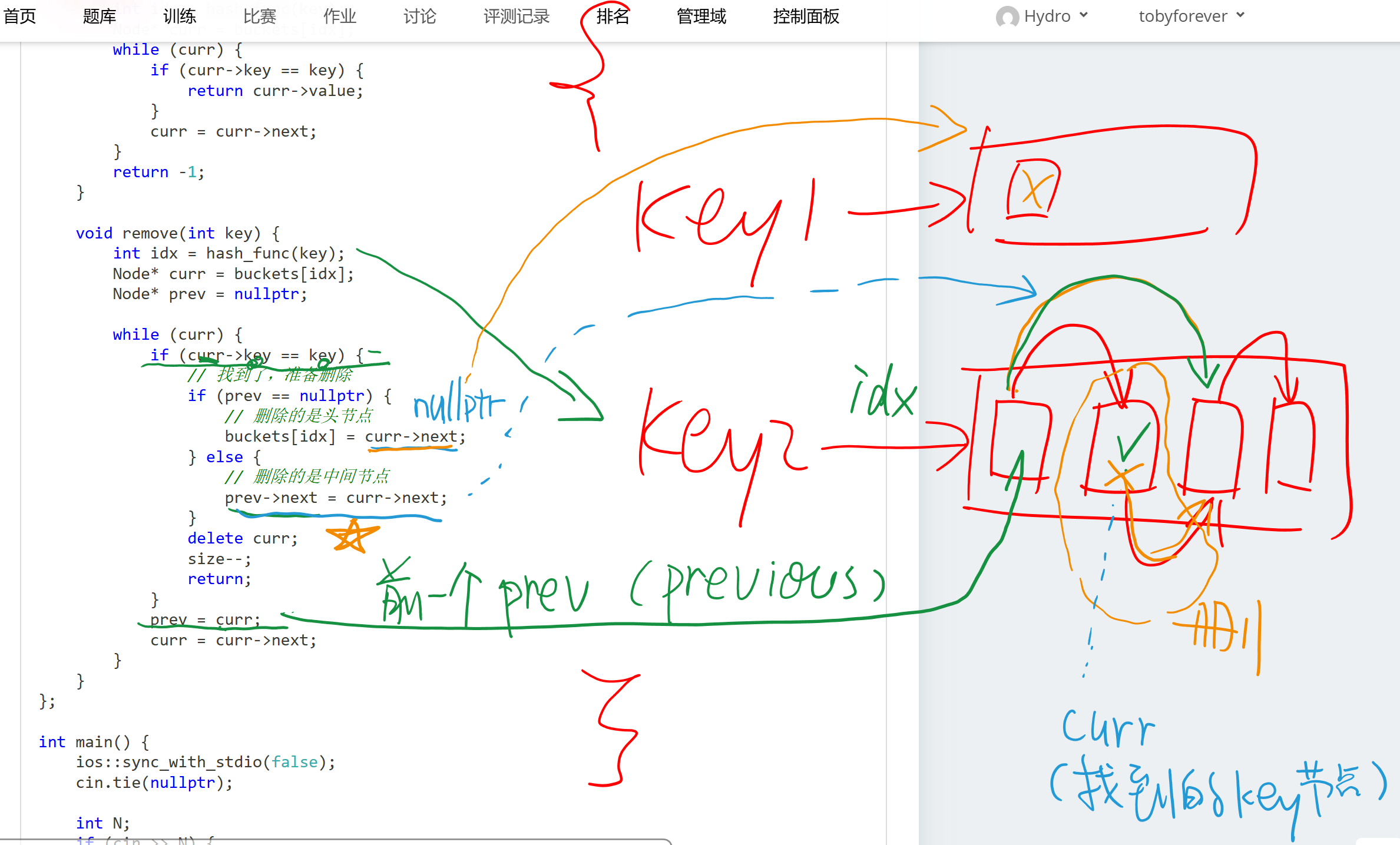
4. 删除 (remove) 的指针技巧：

   • 删除链表节点时，需要把“前一个人的手”牵到“后一个人”身上。
   • 特判：如果删除的是第一个人（头节点），没有“前一个人”，直接把“柜子标签”改成第二个人即可。

哈希表内部结构 / 删除技巧

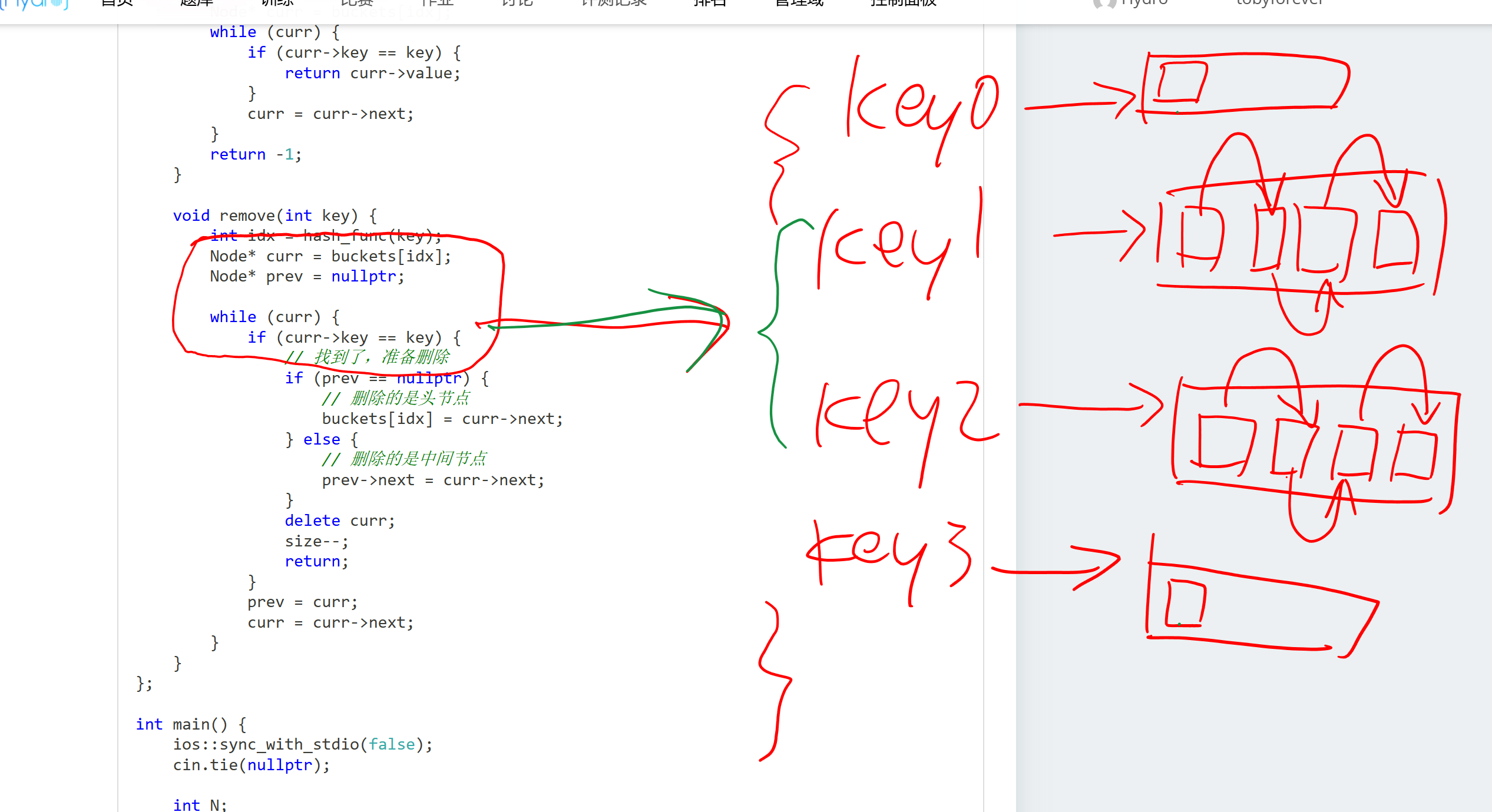
链表删除中间元素