#CF7D. 回文阶数Palindrome Degree
回文阶数Palindrome Degree
你好!我是你的 OI 金牌教练。今天我们来探讨一道将回文性质与 动态规划(DP) 巧妙结合的高阶字符串题目:Codeforces 7D - Palindrome Degree。
在 NOI 系列竞赛(如省选或全国赛)中,当字符串长度达到 这一级别时,对算法的时间常数和空间利用率要求极高。这道题不仅考察你对哈希或回文算法的理解,还考验你对线性递推的掌控力。
一、 题目描述:Palindrome Degree (回文阶数)
【问题描述】 回文阶数的定义如下:
- 任何非回文字符串的阶数均为 。
- 长度为 的字符串是回文串,其阶数为 。
- 对于长度 的字符串 ,如果它是回文串,则它的阶数等于 ,其中 是 的长度为 的前缀。
给定一个字符串 ,求 所有前缀的回文阶数之和。
【输入格式】 输入仅一行,包含一个由字母和数字组成的字符串,长度 。
【输出格式】 输出一个整数,表示该字符串所有前缀的回文阶数之和。
【样例输入】
abacaba
【样例输出】
6
【样例说明】 该字符串的所有前缀及其回文阶数如下:
a: 1ab: 0aba: 2abac: 0abaca: 0abacab: 0abacaba: 3 所有阶数之和为 。
【数据范围与说明】
- 。
- 时间限制:2.0s,内存限制:256MB。
二、 预备知识点
- 字符串哈希 (String Hashing):在 时间内判断两个子串是否相同,或判断前缀是否为回文。
- 动态规划 (DP):利用前缀之间的递推关系减少重复计算。
- 回文性质:理解回文串的对称性及其前缀与后缀的关系。
三、 教学启发与草稿纸推理
1. 启发式提问
- 教练问:要算一个长度为 的前缀的阶数,前提是什么?
- 学生答:前提是这个前缀必须是回文串。
- 教练问:如果 是回文串,它的阶数取决于谁?
- 学生答:取决于它长度为 的前缀的阶数。这看起来像是一个递推式:。
- 教练问:关键问题来了,如何在 总时间内判断所有前缀是否为回文?
2. 草稿纸上的图形化模拟
假设字符串为 。我们要判断 是否为回文,即判断: 前缀 == 翻转后的前缀 。
请在草稿纸上画出两个哈希轨迹:
- 正向哈希 (Forward Hash):从左往右计算,。
- 反向哈希 (Backward Hash):由于我们要动态判断每个前缀,反向哈希可以这样维护:。
当 时,我们初步判定 是回文串。
3. 递推逻辑 (DP)
定义 为前缀 的阶数:
- 如果 :
- 否则:
- 答案:
四、 复杂度分析与建议
- 时间复杂度:。计算哈希和 DP 递推均为线性时间。对于 的数据,建议使用
unsigned long long自然溢出哈希,并使用getchar()或fread提速读取。 - 空间复杂度:。只需要一个数组存储 DP 状态。注意字符串长度很大,不要使用
std::string的频繁拷贝。 - 优化建议:哈希可能存在碰撞。在 NOI 竞赛中,如果怕被卡,可以使用双哈希。但由于本题时限较紧(2s 处理 ),单哈希通常能过。
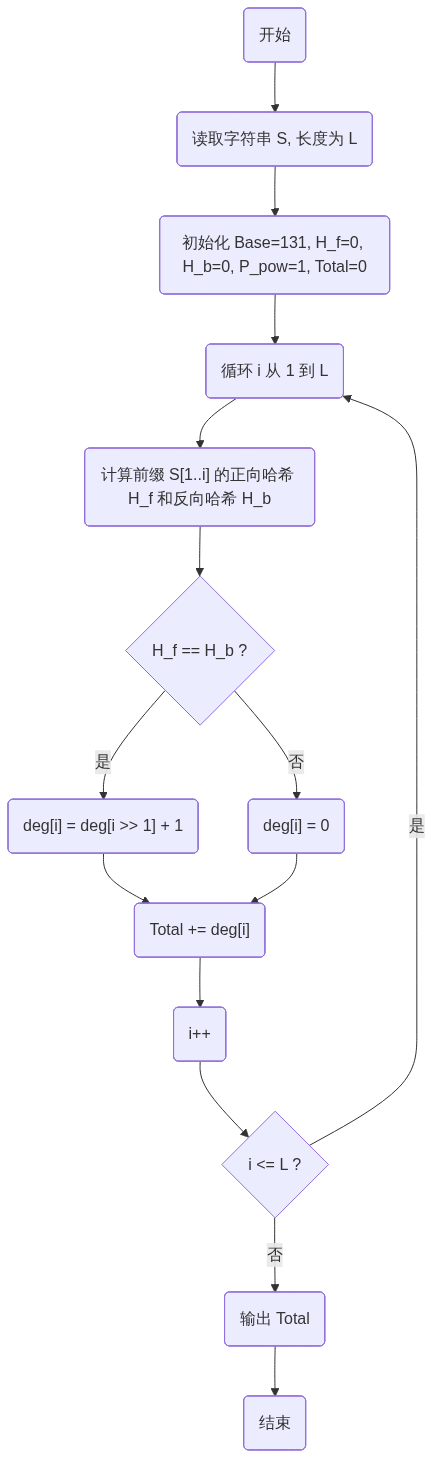
五、 算法流程图 (Mermaid 语法)
graph TD
Start("开始") --> ReadS("读取字符串 S, 长度为 L")
ReadS --> Init("初始化 Base=131, H_f=0, H_b=0, P_pow=1, Total=0")
Init --> Loop("循环 i 从 1 到 L")
Loop --> HashCalc("计算前缀 S[1..i] 的正向哈希 H_f 和反向哈希 H_b")
HashCalc --> IsPalin{"H_f == H_b ?"}
IsPalin -- "是" --> UpdateDeg("deg[i] = deg[i >> 1] + 1")
IsPalin -- "否" --> ZeroDeg("deg[i] = 0")
UpdateDeg --> AddTotal("Total += deg[i]")
ZeroDeg --> AddTotal
AddTotal --> Next("i++")
Next --> LoopCheck{"i <= L ?"}
LoopCheck -- "是" --> Loop
LoopCheck -- "否" --> Print("输出 Total")
Print --> End("结束")
六、 读题关键点总结
在处理这类题目时,关键词决定了你的算法选型:
- “所有前缀” (All prefixes):暗示我们需要一个线性扫描的过程,并实时维护前缀信息。
- “ 的前缀” (Prefix of length n/2):这是经典的 DP 转移标志,说明当前状态可以从之前计算过的状态转移而来。
- “回文” (Palindrome):
- 长度较小时考虑中心扩展。
- 求所有回文子串考虑 Manacher 算法。
- 快速判断前缀回文考虑哈希 (Hashing)。
- (Data Scale):看到这个量级,脑中必须闪过 。任何涉及 且常数较大的算法(如某些复杂的后缀数组实现)都存在风险。
在 NOI 竞赛中,这种“前缀的阶数取决于它一半长度的前缀”是典型的线性 DP 转移。
易错提醒:
- 溢出问题:虽然
abacaba的答案只有 6,但对于 长度的全a字符串,答案会非常大(约为 ),虽然在int范围内,但为了稳妥,NOI 选手通常会使用long long来存储Total。 - 哈希安全性:由于 的数据量非常大,单哈希(如自然溢出)发生碰撞的概率虽然低,但在针对性构造下风险依然存在。双哈希是金牌选手的最后一道保险。
教练点评:这道题是哈希和 DP 的完美结合。在 NOI 中,哈希是解决回文问题的利器,尤其是当你需要判断“特定位置”是否回文时。记住,哈希虽有概率冲突,但在如此大的数据量面前,它是平衡效率与开发难度的最佳选择。加油!