你好，同学。欢迎来到 NOI 提高组专项训练。

今天我们要攻克的是数据结构与哈希应用的经典题目：最长连续序列。这道题的难点在于题目给出了极其苛刻的时间复杂度限制——必须在 $O(n)$ 时间内完成，这排除了我们最常用的 $O(n \log n)$ 排序算法。

一、 预备知识点

在动手前，请确保你已经掌握：

1. 哈希表（Hash Table）：在 C++ STL 中通常使用 std::unordered_set。
   • 其插入与查询的期望时间复杂度均为 $O(1)$。
2. 均摊时间复杂度分析：理解为什么嵌套循环在特定条件下依然是 $O(n)$。
3. 序列去重：处理重复元素对结果的影响。

二、 NOI 竞赛题目描述

题目名称：最长连续序列 (Longest Consecutive Sequence) 时间限制：1.0s 内存限制：256MB

【问题描述】 给定一个长度为 $n$ 的未排序整数数组 nums，请找出其中数字连续的最长序列（不要求序列元素在原数组中连续）的长度。

【要求】 设计并实现时间复杂度为 $O(n)$ 的算法解决此问题。

【输入格式】 输入共两行。 第一行包含一个整数 $n$，表示数组长度。 第二行包含 $n$ 个整数，表示数组中的元素，以空格分隔。

【输出格式】 输出一个整数，表示最长连续序列的长度。

【样例输入】

6
100 4 200 1 3 2

【样例输出】

4

【样例解释】 最长数字连续序列是 [1, 2, 3, 4]，它的长度为 4。

【数据规模与约定】

• $0 \le n \le 10^5$
• $-10^9 \le nums_i \le 10^9$

三、 启发式思路引导：草稿纸上的推演

请拿出草稿纸，我们尝试跳出“排序”的固有思维。

1. 核心矛盾：如何快速定位“连续”？

• 观察：如果数字 x 是一个连续序列的起点，那么 x-1 必然不在原数组中。
• 策略：
  1. 把所有数字丢进一个哈希表（unordered_set），实现 $O(1)$ 查找。
  2. 遍历数组中的每个数字 num。
  3. 寻找起点：判断 num - 1 是否在哈希表中。
     • 如果有，说明 num 只是某个序列的中间成员，跳过它。
     • 如果无，说明 num 是一个潜在序列的绝对起点。
  4. 开始计数：从起点 num 开始，不断查询 num + 1, num + 2 ... 是否在表中。

2. 时间复杂度分析思考（为什么是 $O(n)$？）

• 虽然代码里看起来有嵌套循环（一个 for 配合一个 while），但请注意：
  • 只有当一个数是“起点”时，才会进入 while 循环。
  • 每个数字在整个过程中，只会被 while 循环访问一次。
  • 总的操作次数是 $n$（外部遍历）+ $n$（内部序列累加），即 $O(n)$。

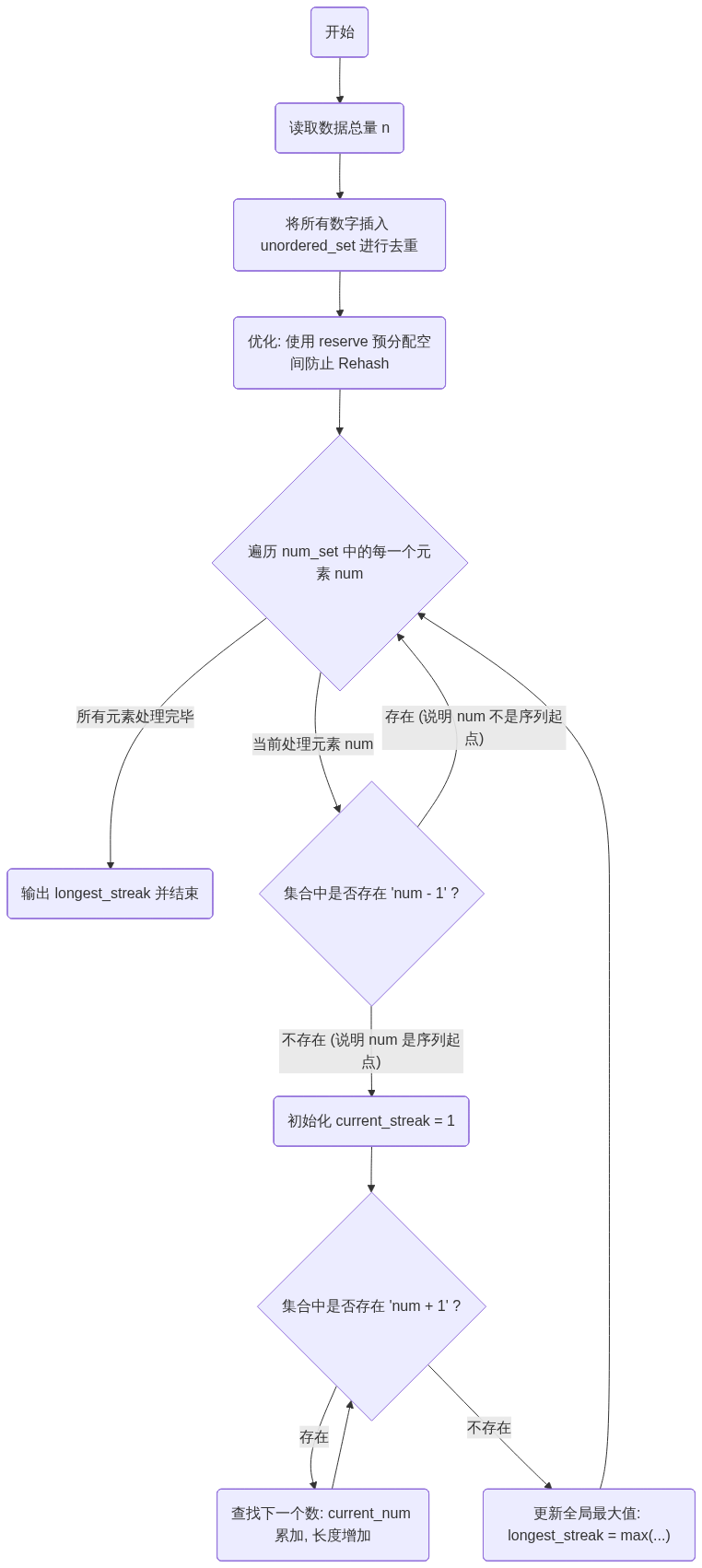
四、 算法流程图（C++14 伪代码表示）

在 Mermaid 流程图中，我们使用通俗描述替代特殊符号，防止渲染报错。

graph TD
    Start(开始处理任务) --> HashSet(将所有数字存入 unordered_set 进行去重和 $O(1)$ 查找)
    HashSet --> OuterLoop{遍历数组中的每个数字 x}
    OuterLoop -- 结束 --> EndResult(输出全局最大长度 max_len)
    
    OuterLoop -- 正在处理 x --> CheckPre{x 减 1 是否存在于集合中}
    
    CheckPre -- 是 --> OuterLoop
    CheckPre -- 否 --> StartCount(说明 x 是序列起点, 初始化 current_len 为 1)
    
    StartCount --> WhileLoop{x 加 1 是否存在于集合中}
    WhileLoop -- 是 --> Increment(x 自增 1, current_len 自增 1)
    Increment --> WhileLoop
    
    WhileLoop -- 否 --> UpdateMax(更新 max_len 为当前长度与原最大值的较大者)
    UpdateMax --> OuterLoop

五、 时间复杂度优化与竞赛建议

1. I/O 优化：在 NOI 考场上，面对 $10^5$ 量级的数据，请务必使用 ios::sync_with_stdio(false); cin.tie(0); 或者 scanf。
2. 空间换时间：unordered_set 的常数略大。如果数据范围集中（例如数值都在 $1 \dots 10^6$ 之间），直接用 bool 数组做桶计数会更快。但本题数值范围达 $10^9$，必须使用哈希表。
3. 内存预分配：
   • 使用 st.reserve(n) 可以避免哈希表频繁重构（Rehash），这是压低运行时间的黑科技。

六、 读题关键词总结

在处理“连续性”或“序列”类题目时，请圈出这些词：

1. “未排序”且“O(n)”：这基本锁定了哈希表或者并查集方案，排除了排序。
2. “连续序列”：意味着数值差值为 1，不同于“子序列”（不要求数值连续）。
3. “数字连续”：注意本题不要求在原数组中的位置连续，只要求数值上的连续。

教练寄语： 这道题体现了**“找到突破口”**的重要性。我们不盲目地对每个数进行搜索，而是通过“判断是否存在 x-1”来过滤掉非起点的无效计算。这种“只处理头部”的思想在很多高级算法（如网络流、图论）中都有体现。去实现它吧！