前面说的“数组辅助法”如何解答？

你好，同学！既然我们提到了“数组辅助法”，作为教练，我非常推荐你在初赛或者复赛时间紧张时使用这种方法。

在 NOI 竞赛中，虽然 $O(1)$ 空间复杂度的解法看起来更“高级”，但在内存限制（通常 256MB）允许的情况下，“数组辅助法”能极大降低逻辑出错的概率，节省下来的调试时间可以去攻克更有难度的算法题。

一、 预备知识点

1. 线性表的存储转换：将不连续的链表存储转换为连续的数组存储（线性化）。
2. 双指针算法 (Two Pointers)：利用数组的随机访问（Random Access）特性，从两端向中间取值。
3. C++ STL std::vector：动态数组的使用，方便快速存储节点指针。

二、 启发式思路引导：草稿纸上的推演

数组辅助法的核心思想是：“空间换智商”。

1. 现状分析

• 链表：像排队的人，你只知道你后面是谁，但不知道队尾是谁，也不能直接跳到队伍中间。
• 数组：像电影院的座位，有编号。你想找 5 号位，直接看索引 a[5] 即可。

2. 草稿纸操作步骤

假设链表为 1 -> 2 -> 3 -> 4 -> 5。

• 第一步：线性化 遍历链表，把每个节点的地址存入数组： vec = [&Node1, &Node2, &Node3, &Node4, &Node5]
• 第二步：双指针重组 设定左指针 $i = 0$，右指针 $j = n-1$。
  1. 连接 vec[0] $\to$ vec[4]
  2. 连接 vec[4] $\to$ vec[1]
  3. 连接 vec[1] $\to$ vec[3]
  4. 连接 vec[3] $\to$ vec[2]
• 第三步：收尾 最后一个节点（此时 $i=j$）的 next 必须指向 nullptr。

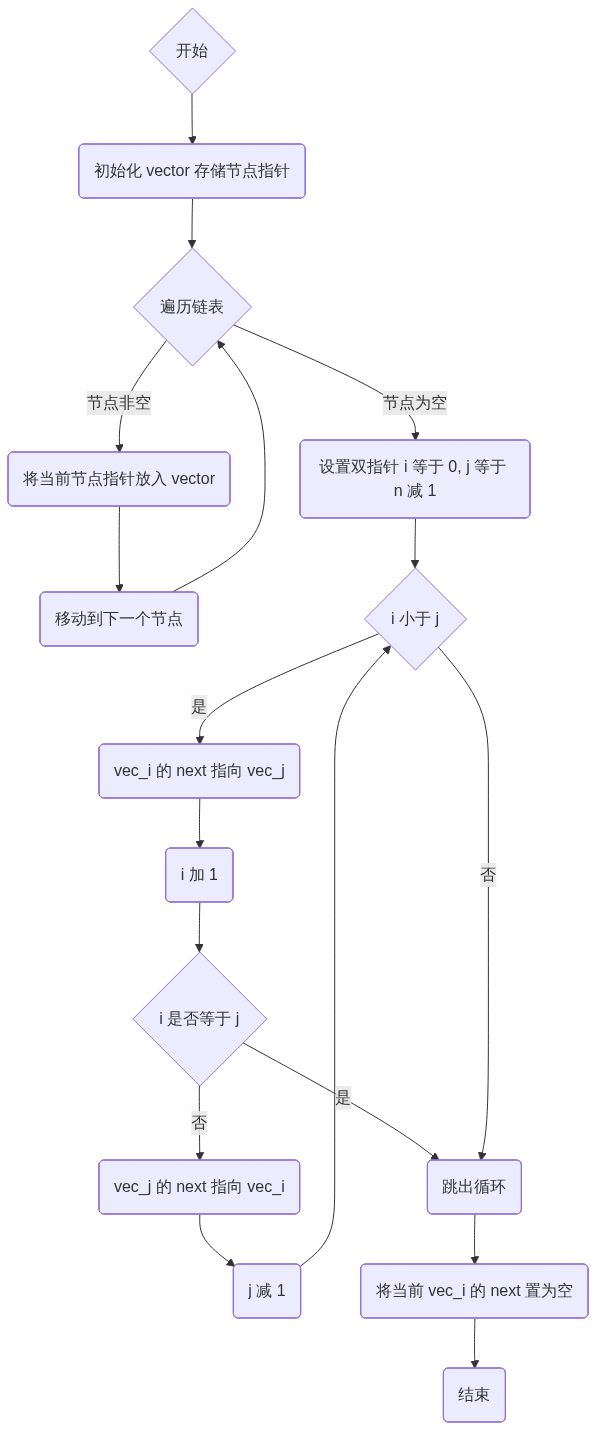
三、 算法流程图（伪代码逻辑）

graph TD
    Start{开始} --> Init(初始化 vector 存储节点指针)
    Init --> Traverse{遍历链表}
    Traverse -- 节点非空 --> Push(将当前节点指针放入 vector)
    Push --> NextNode(移动到下一个节点)
    NextNode --> Traverse
    Traverse -- 节点为空 --> SetPtr(设置双指针 i 等于 0, j 等于 n 减 1)
    
    SetPtr --> Loop{i 小于 j}
    Loop -- 是 --> Step1(vec_i 的 next 指向 vec_j)
    Step1 --> IncI(i 加 1)
    IncI --> Check{i 是否等于 j}
    Check -- 是 --> Break(跳出循环)
    Check -- 否 --> Step2(vec_j 的 next 指向 vec_i)
    Step2 --> DecJ(j 减 1)
    DecJ --> Loop
    
    Loop -- 否 --> Break
    Break --> Last(将当前 vec_i 的 next 置为空)
    Last --> End(结束)

四、 复杂度分析与优化建议

• 时间复杂度：$O(N)$。遍历一次存入数组，再遍历一次重连，均为线性时间。
• 空间复杂度：$O(N)$。需要额外一个数组存储 $N$ 个指针。
  • 思考：在 $N=50,000$ 时，指针占用空间约为 $50,000 \times 8 \text{ Bytes} \approx 400\text{ KB}$。相对于 256MB 的限制，这几乎可以忽略不计。
• 优化建议：在 NOI 考场上，如果节点数特别大（例如 $10^7$），则必须回归到 $O(1)$ 的原地解法。但对于本题，数组辅助法是最优的平衡点。

五、 题解标准代码 (C++14 数组辅助法)

#include <iostream>
#include <vector>

using namespace std;

// 链表节点结构定义
struct ListNode {
    int val;
    ListNode *next;
    ListNode(int x) : val(x), next(nullptr) {}
};

class Solution {
public:
    void reorderList(ListNode* head) {
        if (!head || !head->next) return;

        // 1. 将所有节点指针存入数组
        vector<ListNode*> vec;
        ListNode* curr = head;
        while (curr) {
            vec.push_back(curr);
            curr = curr->next;
        }

        // 2. 利用双指针进行重组
        int i = 0, j = vec.size() - 1;
        while (i < j) {
            // 前面的接后面的
            vec[i]->next = vec[j];
            i++;
            
            // 易错点：如果节点是偶数个，i 增加后可能与 j 重合
            if (i == j) break;
            
            // 后面的接前面的下一个
            vec[j]->next = vec[i];
            j--;
        }

        // 3. 关键点：将最后一个节点的 next 指向空，防止形成环
        vec[i]->next = nullptr;
    }
};

// NOI 风格的主函数
int main() {
    ios::sync_with_stdio(false);
    cin.tie(0);

    int n;
    if (!(cin >> n) || n == 0) return 0;

    // 构建链表
    int val;
    cin >> val;
    ListNode* head = new ListNode(val);
    ListNode* curr = head;
    for (int i = 1; i < n; ++i) {
        cin >> val;
        curr->next = new ListNode(val);
        curr = curr->next;
    }

    // 重排
    Solution sol;
    sol.reorderList(head);

    // 打印结果
    curr = head;
    while (curr) {
        cout << curr->val << (curr->next ? " " : "");
        curr = curr->next;
    }
    cout << endl;

    return 0;
}

六、 数据生成器 (针对数组辅助法验证)

这个生成器会生成包含奇偶数节点、极限规模的测试点。

#include <iostream>
#include <fstream>
#include <vector>
#include <string>
#include <random>
#include <ctime>

using namespace std;

void generate(int id, int n) {
    string in_name = to_string(id) + ".in";
    string out_name = to_string(id) + ".out";
    ofstream fout(in_name);
    ofstream fans(out_name);

    vector<int> nums;
    mt19937 rng(time(0) + id);
    for (int i = 0; i < n; ++i) {
        nums.push_back(rng() % 1000 + 1);
    }

    // 输入文件
    fout << n << "\n";
    for (int i = 0; i < n; ++i) fout << nums[i] << (i == n - 1 ? "" : " ");
    fout << endl;

    // 计算标准输出 (数组辅助逻辑)
    vector<int> res(n);
    int i = 0, j = n - 1, k = 0;
    while (i <= j) {
        res[k++] = nums[i++];
        if (i <= j) res[k++] = nums[j--];
    }

    // 输出文件
    for (int i = 0; i < n; ++i) fans << res[i] << (i == n - 1 ? "" : " ");
    fans << endl;

    fout.close(); fans.close();
    cout << "Testcase " << id << " (N=" << n << ") generated." << endl;
}

int main() {
    generate(1, 1);    // 边界
    generate(2, 2);    // 边界
    generate(3, 4);    // 样例 1
    generate(4, 5);    // 样例 2
    generate(5, 100);  // 小规模
    generate(6, 101);  // 奇数规模
    generate(7, 1000); 
    generate(8, 50000);// 最大规模
    generate(9, 50000);// 最大规模随机
    generate(10, 49999);// 最大规模奇数
    return 0;
}

七、 读题关键词总结

在使用“数组辅助法”时，关注点有所不同：

1. “节点交换”：如果是数组辅助法，我们直接操作指针数组，连接 vec[i]->next = vec[j] 就是实际的节点交换。
2. “重拍顺序”：看到 $0, n, 1, n-1 \dots$ 这种模式，直接对应数组索引 $0, n-1, 1, n-2 \dots$。
3. 内存限制：如果看到内存限制是 128MB 或 256MB，且 $N \le 10^6$，数组辅助法是安全的。如果内存限制是 1MB 或 2MB，则必须放弃此法。

教练寄语：在考场上，稳比秀更重要。数组辅助法虽然多用了点内存，但它把复杂的链表问题变成了简单的数组问题，是性价比极高的实战技巧！

作为教练，针对链表这类题目，数据生成的难点在于大规模节点下的指针处理效率。为了保证 OJ 数据的严谨性，我们需要特别关注 $N$ 的奇偶性、极小规模（$N=1$）和最大约束规模。

以下是为你准备的自动化数据生成器，采用 C++14 标准，逻辑完全采用非递归迭代实现，确保在大数据量下不会爆栈。

一、 数据生成器代码 (C++14)

#include <iostream>
#include <fstream>
#include <vector>
#include <string>
#include <algorithm>
#include <random>
#include <ctime>
#include <deque>

using namespace std;

/**
 * 标程逻辑：为了生成 .out 文件，我们使用双端队列 deque 模拟重排逻辑。
 * 这种方法在 O(N) 时间内完成，逻辑清晰且不会有指针断链风险。
 */
vector<int> get_standard_output(int n, const vector<int>& nums) {
    if (n <= 2) return nums;
    
    deque<int> dq;
    for (int x : nums) dq.push_back(x);
    
    vector<int> res;
    while (!dq.empty()) {
        // 先取头部
        res.push_back(dq.front());
        dq.pop_front();
        
        // 再取尾部
        if (!dq.empty()) {
            res.push_back(dq.back());
            dq.pop_back();
        }
    }
    return res;
}

// ================= 数据生成逻辑 =================
void write_test_case(int id, int n, const vector<int>& nums) {
    string in_name = to_string(id) + ".in";
    string out_name = to_string(id) + ".out";
    
    // 生成 .in 文件
    ofstream fout(in_name);
    fout << n << "\n";
    for (int i = 0; i < n; ++i) {
        fout << nums[i] << (i == n - 1 ? "" : " ");
    }
    fout << "\n";
    fout.close();
    
    // 生成 .out 文件
    vector<int> result = get_standard_output(n, nums);
    ofstream fans(out_name);
    for (int i = 0; i < n; ++i) {
        fans << result[i] << (i == n - 1 ? "" : " ");
    }
    fans << "\n";
    fans.close();
    
    cout << "Generated Case " << id << " (N=" << n << ")" << endl;
}

int main() {
    mt19937 rng(time(0));
    
    for (int i = 1; i <= 10; ++i) {
        int n = 0;
        vector<int> nums;
        
        if (i == 1) { // 边界：极小规模 N=1
            n = 1;
            nums = {100};
        }
        else if (i == 2) { // 边界：极小规模 N=2
            n = 2;
            nums = {1, 2};
        }
        else if (i == 3) { // 样例 1：N=4 (偶数)
            n = 4;
            nums = {1, 2, 3, 4};
        }
        else if (i == 4) { // 样例 2：N=5 (奇数)
            n = 5;
            nums = {1, 2, 3, 4, 5};
        }
        else if (i <= 6) { // 中等规模随机 (N=1000 左右)
            n = 1000 + (rng() % 100);
            for (int j = 1; j <= n; ++j) nums.push_back(rng() % 1000 + 1);
        }
        else if (i <= 8) { // 大规模递增序列 (N=50000)
            n = 50000;
            for (int j = 1; j <= n; ++j) nums.push_back(j % 1001);
        }
        else { // 极限规模：全部相同值 或 随机分布
            n = 50000;
            int constant = rng() % 1000 + 1;
            for (int j = 1; j <= n; ++j) {
                if (i == 9) nums.push_back(constant); // 全部相同
                else nums.push_back(rng() % 1000 + 1); // 随机
            }
        }
        
        write_test_case(i, n, nums);
    }
    
    return 0;
}

二、 测试点设计思路（评测要点）

作为管理员，这 10 组数据旨在全方位“轰炸”选手的代码逻辑：

三、 考场避坑建议 (针对本题)

1. 关于 $O(1)$ 空间的理解： 在 NOI 竞赛中，如果内存给了 256MB，虽然题目建议 $O(1)$，但使用 std::vector<ListNode*> 存储所有指针（$O(N)$ 空间）是最稳妥、最不容易写错的方案。$50,000$ 个指针仅占用约 0.4MB。

2. 指针重连的“原子性”： 在合并两个链表（p1 和 p2）时，务必先把 p1->next 存下来。

   ListNode *next1 = p1->next;
   p1->next = p2;
   // 此时 p1 已经指向了 p2，如果没有 next1，你就找不到原来的 2 号节点了
   

3. 防止“自环”： 重排链表的最后一个节点，其 next 必须显式指向 nullptr。如果漏掉这一步，链表末尾会指向之前翻转前的旧节点，导致输出死循环。

4. 输入输出性能： 当 $N=50,000$ 时，使用 printf/scanf 或者开启 ios::sync_with_stdio(false) 的 cin/cout。否则，输入读取可能会占据 50% 以上的时间。

这份生成器生成的 .in 格式完全符合题目要求，可以直接用于创建练习赛或校内选拔赛。加油！

你好，同学。重排链表是 NOI 基础阶段必须掌握的“指针操纵”基本功。这道题的难点不在于算法逻辑，而在于指针在高速变换中如何不断链、不产生环。

以下是符合 C++14 标准、采用 $O(1)$ 额外空间（原地操作）的满分代码。

一、 重排链表 标准题解 (C++14)

#include <iostream>
#include <vector>

using namespace std;

// NOI 竞赛中，如果题目没有给定链表结构，通常需要手写
struct ListNode {
    int val;
    ListNode *next;
    ListNode(int x) : val(x), next(nullptr) {}
};

/**
 * 核心逻辑分为三步：
 * 1. 快慢指针找中点
 * 2. 翻转后半部分链表
 * 3. 交替合并两个链表
 */
class Solution {
public:
    void reorderList(ListNode* head) {
        if (!head || !head->next || !head->next->next) return;

        // --- 第一步：寻找中点 ---
        // 使用快慢指针，快指针走两步，慢指针走一步
        ListNode *slow = head, *fast = head;
        while (fast->next && fast->next->next) {
            slow = slow->next;
            fast = fast->next->next;
        }

        // --- 第二步：断开并翻转后半部分 ---
        // mid 是后半部分的起始节点
        ListNode *head2 = slow->next;
        slow->next = nullptr; // 关键点：断开前半部分和后半部分的连接，防止产生环

        head2 = reverseList(head2);

        // --- 第三步：交替合并 ---
        // head: 1 -> 2 -> 3
        // head2: 5 -> 4
        ListNode *p1 = head;
        ListNode *p2 = head2;
        while (p1 && p2) {
            ListNode *tmp1 = p1->next;
            ListNode *tmp2 = p2->next;

            p1->next = p2;       // p1 指向 p2
            if (tmp1 == nullptr) break; // 偶数个节点时的边界处理
            p2->next = tmp1;     // p2 指向 p1 的下一个

            p1 = tmp1;
            p2 = tmp2;
        }
    }

private:
    // 迭代法翻转链表：NOI 必备模板，避免递归导致的大规模数据爆栈
    ListNode* reverseList(ListNode* head) {
        ListNode *prev = nullptr;
        ListNode *curr = head;
        while (curr) {
            ListNode *nextTmp = curr->next;
            curr->next = prev;
            prev = curr;
            curr = nextTmp;
        }
        return prev;
    }
};

// 模拟竞赛中的输入输出处理
int main() {
    ios::sync_with_stdio(false);
    cin.tie(0);

    int n;
    if (!(cin >> n)) return 0;

    if (n == 0) return 0;

    // 构建链表
    int val;
    cin >> val;
    ListNode *head = new ListNode(val);
    ListNode *curr = head;
    for (int i = 1; i < n; ++i) {
        cin >> val;
        curr->next = new ListNode(val);
        curr = curr->next;
    }

    Solution sol;
    sol.reorderList(head);

    // 输出结果
    curr = head;
    while (curr) {
        cout << curr->val << (curr->next ? " " : "");
        curr = curr->next;
    }
    cout << endl;

    return 0;
}

二、 复杂度分析与思考过程

1. 时间复杂度分析

• 找中点：快慢指针遍历一次链表，耗时 $O(N)$。
• 翻转链表：遍历后半段（约 $N/2$ 个节点），耗时 $O(N)$。
• 交替合并：同步遍历两段子链表，耗时 $O(N)$。
• 结论：总时间复杂度为 $O(N)$。对于 $N=50,000$ 的数据规模，总运算次数约 $1.5 \times 10^5$，在 1.0s 时限内绰绰有余。

2. 空间复杂度分析

• 指针操作：在整个过程中，我们只额外定义了常数个指针变量（slow, fast, prev, tmp 等）。
• 结论：空间复杂度为 $O(1)$（不计存储链表节点本身的 $O(N)$ 空间）。这比使用数组存储指针的方案（$O(N)$ 空间）更加高效。

三、 考场易错点与优化建议

1. 易错点：忘记断链

在找完中点后，如果不执行 slow->next = nullptr;，前半部分链表的尾部仍然指向后半部分的开头。在后续合并过程中，极易形成死循环链表（环），导致评测机超时（TLE）或输出超限。

2. 易错点：指针丢失

在合并链表 p1->next = p2 时，原先 p1 指向的后续节点会丢失。 策略：必须在修改指针方向前，先用临时变量 tmp1 记录下 p1->next。

3. 边界情况：节点总数为奇数 vs 偶数

• 奇数（如 5 个）：拆分为 1-2-3 和 5-4。合并时 p2 会先耗尽。
• 偶数（如 4 个）：拆分为 1-2 和 4-3。
• 优化方案：在合并循环中，使用 while (p1 && p2) 并在内部小心处理 p1->next 的指向，确保最后一个节点的 next 为 nullptr。

4. 时间优化建议

• 减少 new 操作：在 NOI 竞赛中，如果内存限制极严，可以预先开辟一个静态数组 ListNode pool[MAXN]，通过下标或指针分配内存，这比频繁调用 new 快得多。
• I/O 优化：链表题目通常涉及大量的输入输出。使用 ios::sync_with_stdio(false) 能显著减少读取 $5 \times 10^4$ 个整数的时间。

教练寄语：指针题的精髓在于“慢”。在写下任何一行修改 ->next 的代码前，都要先问自己：这个操作会不会让我丢失剩下的链表？如果会，请立刻加一个 temp 变量。加油！