你好，同学！欢迎来到 NOI 专题训练。

今天我们要攻克的是滑动窗口与单调队列结合的经典进阶题：绝对差不超过限制的最长连续子数组。这道题在 NOI 竞赛中属于中档偏易的题目，但它考查的“双单调队列维护区间最值”是解决许多复杂 DP 优化的前置技能。

一、 预备知识点

1. 滑动窗口（Sliding Window）：用于维护一个动态的连续区间。
2. 单调队列（Monotonic Queue）：在 $O(1)$ 时间内获取当前区间的最大值和最小值。
3. 双指针算法：通过左指针 left 和右指针 right 的移动来调整区间长度。

二、 NOI 竞赛题目描述

题目名称：绝对差不超过限制的最长连续子数组 时间限制：1.0s 内存限制：256MB

【问题描述】 给定一个长度为 $n$ 的整数数组 nums，以及一个表示限制的整数 limit。 请你返回最长连续子数组的长度，该子数组中的任意两个元素之间的绝对差必须小于或者等于 limit。 如果不存在满足条件的子数组，则返回 $0$。

注意：任意两个元素的绝对差 $\le limit$，等价于该子数组中的 最大值 - 最小值 $\le limit$。

【输入格式】 第一行包含两个整数 $n$ 和 $limit$。 第二行包含 $n$ 个整数，表示数组 nums 的元素。

【输出格式】 输出一个整数，表示满足条件的最长子数组的长度。

【样例输入 1】

4 4
8 2 4 7

【样例输出 1】

2 

(解释：对于 [2,4] 最大差为 2 <= 4；对于 [4,7] 最大差为 3 <= 4；最长长度为 2)

【样例输入 2】

6 5
10 1 2 4 7 2

【样例输出 2】

4

(解释：子数组 [1,2,4,7] 最大差为 7-1=6 > 5 不满足；但 [2,4,7,2] 最大差为 7-2=5 <= 5 满足。)

【数据规模与约定】

• $1 \le n \le 10^5$
• $1 \le nums[i] \le 10^9$
• $0 \le limit \le 10^9$

三、 启发式思路引导：草稿纸上的推演

请在草稿纸上画出两个单调队列的变动过程。

1. 核心矛盾：如何快速获取区间的 $\max$ 和 $\min$？

• 想法 A：每次移动窗口都遍历一遍。复杂度 $O(n^2)$，面对 $10^5$ 数据会超时。
• 想法 B：使用 std::multiset（平衡树）。复杂度 $O(n \log n)$，可以通过，但常数略大。
• 金牌解法：使用两个单调队列。一个维护窗口内递减序列（队首为最大值），一个维护递增序列（队首为最小值）。复杂度 $O(n)$。

2. 双指针逻辑

• 右指针 right 不断向右移动，将新元素加入两个单调队列。
• 检查：如果此时 max_queue.front() - min_queue.front() > limit，说明当前窗口不合法。
• 收缩：左指针 left 向右移动，并同步弹出单调队列中下标小于 left 的元素，直到窗口重新合法。
• 统计：每次移动右指针后，记录 right - left + 1 的最大值。

四、 复杂度分析与时间复杂度优化建议

1. 时间复杂度：
   • 双单调队列：每个元素最多入队一次，出队一次。总复杂度为 $O(n)$。
   • 平衡树（Multiset）：每次插入删除 $O(\log n)$，总复杂度 $O(n \log n)$。
2. 空间复杂度：$O(n)$，用于存储单调队列的下标或数值。
3. NOI 优化建议：
   • 虽然 STL 的 std::deque 很方便，但在 $10^5$ 规模下，手动用数组模拟双端队列（使用 head 和 tail 指针）能显著降低运行常数。
   • 对于数值范围较大的 $nums[i]$，注意做差时是否会产生负数（虽然本题取绝对值后是正数，但养成习惯）。

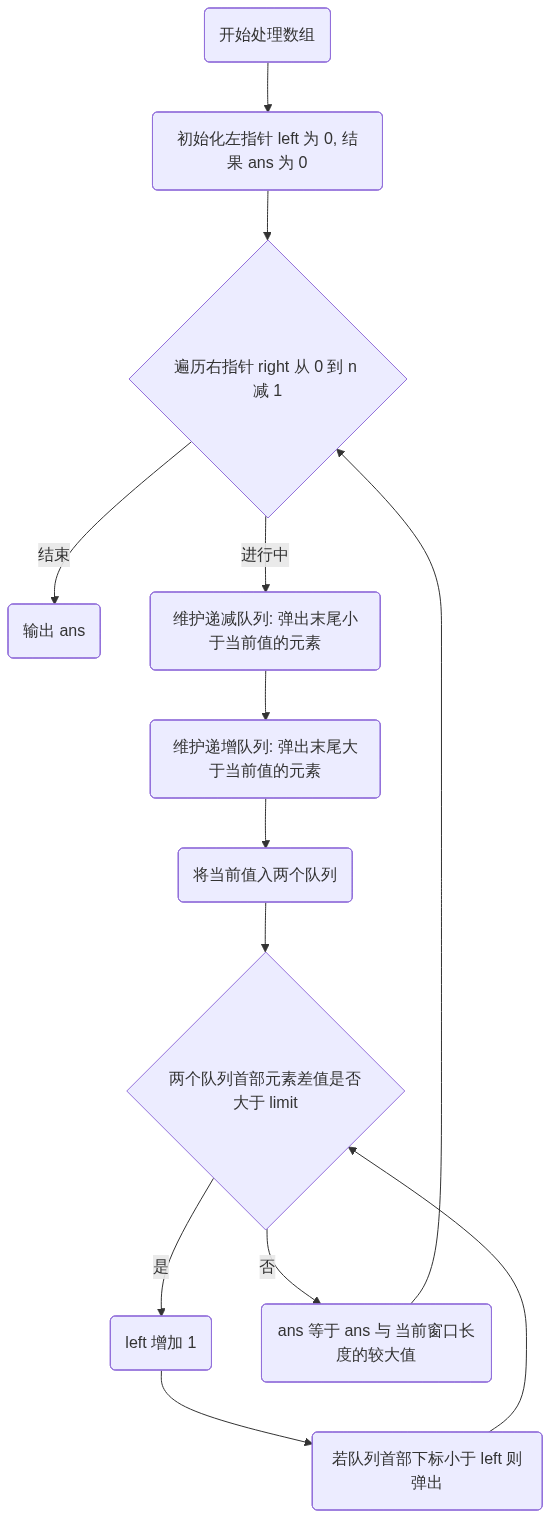
五、 算法流程图（伪代码逻辑）

在流程图中，我们使用通俗描述替代特殊符号，防止渲染报错。

graph TD
    Start(开始处理数组) --> Init(初始化左指针 left 为 0, 结果 ans 为 0)
    Init --> OuterLoop{遍历右指针 right 从 0 到 n 减 1}
    OuterLoop -- 结束 --> EndResult(输出 ans)
    
    OuterLoop -- 进行中 --> MaintainMax(维护递减队列: 弹出末尾小于当前值的元素)
    MaintainMax --> MaintainMin(维护递增队列: 弹出末尾大于当前值的元素)
    MaintainMin --> AddToQueues(将当前值入两个队列)
    
    AddToQueues --> CheckLimit{两个队列首部元素差值是否大于 limit}
    CheckLimit -- 是 --> ShrinkLeft(left 增加 1)
    ShrinkLeft --> PopQueues(若队列首部下标小于 left 则弹出)
    PopQueues --> CheckLimit
    
    CheckLimit -- 否 --> UpdateAns(ans 等于 ans 与 当前窗口长度的较大值)
    UpdateAns --> OuterLoop

六、 读题关键词总结

在 NOI 竞赛中，通过以下词汇快速锁定该题型：

1. “连续子数组”：提示使用滑动窗口或双指针。
2. “任意两个元素之差”：在连续区间内，这等价于区间内最大值与最小值的差。
3. “绝对差不超过限制”：这是一个区间合法性的约束条件。
4. “最长长度”：典型的最优化问题。

教练寄语： 单调队列不仅仅是用来找滑动窗口最大值的，它真正的威力在于能够同时维护多个区间属性。当你能熟练地在草稿纸上模拟出两个队列随着指针“同向赛跑”的过程时，你就已经掌握了这道题的精髓。去实现它吧！