你好，同学。欢迎进入 NOI 专题训练。今天我们要攻克的是组合搜索中的一个经典变体——组合总和 III (Combination Sum III)。

在之前的训练中，我们处理过元素不限次数选取的组合，而这一题则加入了“元素范围固定”、“元素个数固定”且“不可重复使用”的约束。这在 NOI 竞赛中属于典型的限定深度的子集搜索。

一、 题目描述 (NOI 风格)

题目名称：组合总和 III (Combination Sum III) 时间限制：1.0s 内存限制：256MB

【问题描述】 找出所有相加之和为 $n$ 的 $k$ 个数的组合。组合需满足以下条件：

1. 只使用数字 $1$ 到 $9$。
2. 每个数字最多使用一次。
3. 解集中不能包含重复的组合。

【输入格式】 输入仅一行，包含两个整数 $k$ 和 $n$，分别表示组合中数字的个数和目标总和。

【输出格式】 输出若干行，每行表示一个符合条件的组合。元素之间用空格隔开（建议按升序排列组合内的数字）。如果不存在满足条件的组合，则不输出。

【样例输入】

3 7

【样例输出】

1 2 4

【数据说明】 对于 $100\%$ 的数据：$2 \le k \le 9$，$1 \le n \le 45$。

二、 预备知识点

1. 回溯算法 (Backtracking)：在决策树上通过 DFS 寻找所有解。
2. 组合去重技巧：通过维护一个递增的起始索引 start，确保选出的序列是升序的，从而避免产生如 {1, 2} 和 {2, 1} 这样的重复组合。
3. 可行性剪枝 (Feasibility Pruning)：在搜索过程中，如果当前数字和已经超过 $n$，或者剩余数字全选最大的也不够 $n$，则提前返回。

三、 启发式思路引导：草稿纸上的推理过程

请拿出草稿纸，我们以 $k=3, n=9$ 为例来推导。

1. 状态表示

我们需要记录三个核心状态：

• start：当前可以从哪个数字开始选（为了不选重复，我们只往后选）。
• remain_k：还需要选几个数。
• remain_sum：还需要凑多少和。

2. 搜索树推导

• 第一层：我们尝试选 1。
  • 状态变为：start=2, remain_k=2, remain_sum=8。
  • 第二层：尝试选 2。
    • 状态变为：start=3, remain_k=1, remain_sum=6。
    • 第三层：只能选 6。
    • 记录结果：{1, 2, 6}。
• 回溯：回到第二层，不选 2，尝试选 3。
  • 状态变为：start=4, remain_k=1, remain_sum=5。
  • 第三层：尝试选 5。
  • 记录结果：{1, 3, 5}。

3. 剪枝思考 (提分关键)

如果在某一处，你发现：

• remain_sum < 0：当前和已经超了，砍掉！
• remain_k == 0 但 remain_sum != 0：数够了但和不对，砍掉！
• 当前数字 i 已经比 remain_sum 大了：后面的数更大，更不可能凑齐，砍掉！

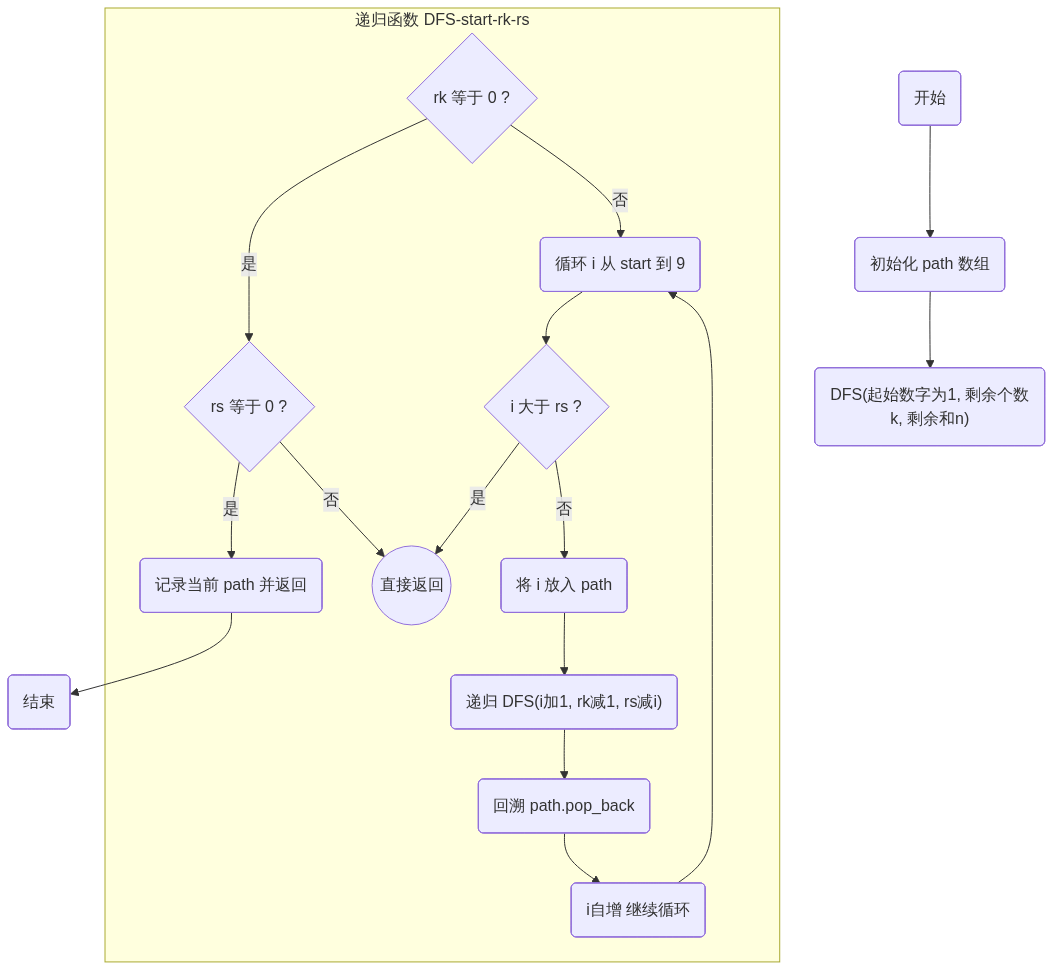
四、 算法流程图 (C++14 伪代码)

为了在 Mermaid 中正常渲染，我们规避了特殊字符。

graph TD
    Start(开始) --> Init(初始化 path 数组)
    Init --> CallDFS("DFS(起始数字为1, 剩余个数k, 剩余和n)")

    subgraph DFS_Process [递归函数 DFS-start-rk-rs]
    CheckK{rk 等于 0 ?}
    CheckK -- 是 --> CheckSum{rs 等于 0 ?}
    CheckSum -- 是 --> Save(记录当前 path 并返回)
    CheckSum -- 否 --> Return((直接返回))
    
    CheckK -- 否 --> LoopInit("循环 i 从 start 到 9")
    LoopInit --> Prune{i 大于 rs ?}
    Prune -- 是 --> Return
    Prune -- 否 --> Action("将 i 放入 path")
    
    Action --> Recur("递归 DFS(i加1, rk减1, rs减i)")
    Recur --> Pop("回溯 path.pop_back")
    Pop --> NextI("i自增 继续循环")
    NextI --> LoopInit
    end

    Save --> End(结束)

五、 复杂度分析与建议

• 时间复杂度分析：

  • 由于数字范围限定在 $1 \dots 9$，且每个数只能用一次，总的状态空间是组合数 $C_9^k$。
  • $C_9^k$ 的最大值出现在 $k=4$ 或 $k=5$ 时，即 $C_9^4 = 126$。
  • 对于每个合法解，输出耗时 $O(k)$。
  • 结论：总复杂度 $O(k \cdot C_9^k)$。由于 $C_9^k$ 极小，此算法在 1.0s 内绰绰有余。

• 空间复杂度分析：

  • 递归深度最大为 $k$（最大为 9）。
  • 辅助数组 path 长度为 $k$。
  • 空间复杂度 $O(k)$，在 256MB 限制下微不足道。

六、 读题理解关键词总结

做 NOI 搜索类题目时，扫描到以下关键词要迅速形成思路：

1. “组合” (Combination)：不是排列。意味着顺序不重要，代码中必须使用 start 索引，禁止走回头路，以防选出 {1, 2} 后又选出 {2, 1}。
2. “最多使用一次” (Unique elements)：DFS 递归时，下一层的起始位置是 i + 1 而不是 i。
3. “1 到 9” (Range limit)：搜索范围非常窄，暗示可以直接暴力回溯。
4. “相加之和为 n” (Sum target)：这是最强的可行性剪枝信号。在循环中如果 i > remain_sum 即可直接 break。

教练寄语： 同学，这道题是搜索算法的“模型拆解”练习。它将组合逻辑、深度限制和目标和限制结合在了一起。只要你能在草稿纸上清晰地画出那棵“不走回头路”的搜索树，这种题目就是送分题。加油！