你好，同学。此前我们讨论过用“双指针”法来解决“接雨水”问题，那是通过维护左右两端最大高度来“按列”计算水量的。

今天，我们要学习的是单调栈解法。在 NOI 竞赛中，这种方法提供了一种全新的视角：按行（横向）计算水量的“填坑法”。这种思维在处理复杂的直方图或物理模拟题时非常有用。

【题目描述】接雨水 (Trapping Rain Water)

题目背景： 由于强降雨，一个地形复杂的山谷出现了积水。我们需要根据给出的地形高度图，计算该山谷一共能蓄多少单位的雨水。

问题描述： 给定 $n$ 个非负整数表示每个柱子的高度，每个柱子的宽度为 1，计算下雨之后这个地形能接多少单位的雨水。

输入格式： 第一行包含一个整数 $n$，表示柱子的数量。 第二行包含 $n$ 个非负整数 $h_i$，用空格隔开，表示高度。

输出格式： 输出一个整数，表示总积水量。

样例输入：

12
0 1 0 2 1 0 1 3 2 1 2 1

样例输出：

6

数据范围： 对于 $100\%$ 的数据：$1 \le n \le 10^5$，$0 \le h_i \le 10^5$。 内存限制：256MB，时间限制：1s。

一、 预备知识点

1. 单调栈 (Monotonic Stack)：本题维护一个单调递减栈（从栈底到栈顶高度递减）。
2. 横向求积法：与双指针的纵向求和不同，单调栈是在发现“凹槽”时，横向计算这一层的储水量。
3. 几何思维：理解“左墙”、“右墙”与“坑底”构成的 U 型结构。

二、 启发式教学：草稿纸上的推演

请拿出草稿纸，我们画出高度序列 [2, 1, 0, 1, 3]：

1. 寻找“凹槽”

• 当我们遇到一个高度，它大于栈顶高度时，说明可能形成了一个“坑”。
• 比如此时栈里存的是 2, 1, 0 的下标，当前遇到 1。1 比 0 高，这就是我们要找的“右墙”。

2. 识别三要素

在草稿纸上圈出这三个关键位置：

• 坑底 (Bottom)：当前被弹出的栈顶元素（高度为 0）。
• 左墙 (Left)：弹出坑底后，新的栈顶元素（高度为 1）。
• 右墙 (Right)：当前遍历到的元素（高度为 1）。

3. 计算这一层的水量

横向水量的公式：

• 高度 (Height)：取左右两墙的较小值，减去坑底的高度。$H = \min(h[Left], h[Right]) - h[Bottom]$。
• 宽度 (Width)：右墙下标减去左墙下标再减一。$W = Right - Left - 1$。
• 水量：$H \times W$。

4. 为什么是横向的？

请在纸上画一下： 当处理 [2, 1, 0, 1, 3] 时：

1. 遇到第一个 1，填平了 0 那一层的坑，得到 $1 \times 1 = 1$ 单位水。
2. 此时高度变成 [2, 1, 1, 3]。继续遇到 3，它比 1 高，再次触发。
3. 填平 1 这一层，左墙是 2，右墙是 3，高度差 $2-1=1$，宽度 $4-0-1=3$，得到 $1 \times 3 = 3$ 单位水。
4. 总计 $1 + 3 = 4$。

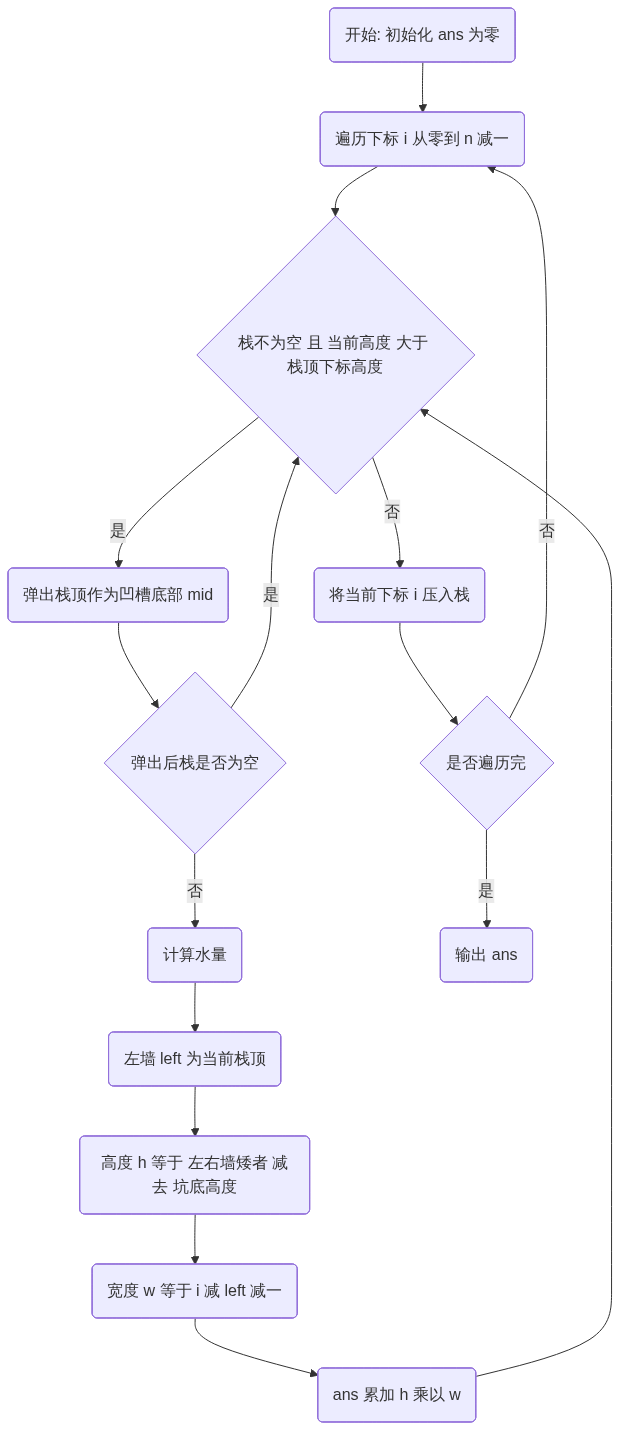
三、 算法流程图 (C++14 伪代码思路)

graph TD
    Start(开始: 初始化 ans 为零) --> Loop(遍历下标 i 从零到 n 减一)
    Loop --> WhileCond{栈不为空 且 当前高度 大于 栈顶下标高度}
    WhileCond -- 是 --> PopBottom(弹出栈顶作为凹槽底部 mid)
    PopBottom --> CheckStack{弹出后栈是否为空}
    CheckStack -- 是 --> WhileCond
    CheckStack -- 否 --> CalcWater(计算水量)
    CalcWater --> GetL(左墙 left 为当前栈顶)
    GetL --> GetH(高度 h 等于 左右墙矮者 减去 坑底高度)
    GetH --> GetW(宽度 w 等于 i 减 left 减一)
    GetW --> Accumulate(ans 累加 h 乘以 w)
    Accumulate --> WhileCond
    WhileCond -- 否 --> Push(将当前下标 i 压入栈)
    Push --> CheckEnd{是否遍历完}
    CheckEnd -- 否 --> Loop
    CheckEnd -- 是 --> Output(输出 ans)

四、 读题关键词总结 (题眼)

1. “接雨水/蓄水”：考察对“凹处”的捕捉。
2. “柱子/直方图”：暗示单调栈是一个潜在的高效工具。
3. “总单位数”：通常暗示 $O(n)$ 复杂度，对于 $10^5$ 的数据，双指针或单调栈都是标准解法。

五、 复杂度分析与优化建议

• 时间复杂度：$O(n)$。每个元素入栈一次，出栈一次。
• 空间复杂度：$O(n)$。最坏情况下（单调递减的地形），栈会存储所有下标。
• 优化建议：
  • 在 NOI 比赛中，若 $N$ 很大，尽量使用手写数组模拟栈以规避 std::stack 的常数开销。
  • 注意高度差计算时可能出现 0 的情况（左右墙一样高或有平地），但在代码逻辑中 $H \times W$ 会自然处理。

教练点评：单调栈解法相比双指针，在处理“接雨水”时更具通用性，比如在某些变体题中要求计算“每一层”的蓄水量，单调栈是唯一的选择。务必熟练掌握这种“找左墙、找右墙”的思维。