你好，同学。很高兴看到你开始挑战经典的单调性问题。在NOI（全国青少年信息学奥林匹克）中，处理“寻找最近的更大/更小元素”是进阶数据结构的基础。

下面我将以金牌教练的视角，为你剖析这道题目。

---

一、 题目描述 (NOI 竞赛风格)

题目名称：下一个更大元素 I (Next Greater Element I) 时间限制：1.0s 内存限制：256MB

【问题描述】 给定两个不包含重复元素的整数数组 nums1 和 nums2 ，其中 nums1 是 nums2 的子集。 对于 nums1 中的每个元素 nums1[i]，找出其在 nums2 中对应位置右侧的第一个比它大的元素。 如果在 nums2 中不存在这样的元素，则该位置输出 $-1$。

【输入格式】 输入文件名为 next.in。 第一行包含两个整数 $n$ 和 $m$，分别表示 nums1 和 nums2 的长度。 第二行包含 $n$ 个整数，表示 nums1 的元素。 第三行包含 $m$ 个整数，表示 nums2 的元素。

【输出格式】 输出到文件 next.out。 输出一行 $n$ 个整数，用空格隔开，表示对应的“下一个更大元素”。

【样例 1 输入】

3 4
4 1 2
1 3 4 2

【样例 1 输出】

-1 3 -1

【数据范围】

• $1 \le n \le m \le 1000$
• $0 \le nums1[i], nums2[i] \le 10^4$
• nums1 和 nums2 中所有整数互不相同。

---

二、 预备知识点

1. 栈 (Stack)：后进先出 (LIFO) 的线性数据结构。

2. 单调栈 (Monotonic Stack)：一种特殊的栈，栈内元素始终保持单调递增或单调递减。它是解决“寻找右侧/左侧第一个大于/小于值”问题的 $O(N)$ 神器。

3. 哈希映射 (Hash Map / std::unordered_map)：用于快速建立 nums2 元素与其“下一个更大元素”之间的映射关系。

---

三、 启发式思维引导 (草稿纸上的推演)

第一步：暴力思考 (Brute Force)

如果我们要直接解，思路是：遍历 nums1 中的每个数 $x$，在 nums2 中先找到 $x$ 的位置，再往右扫描。

• 时间复杂度分析：找位置 $O(M)$，往右扫 $O(M)$，总共 $N$ 个数，复杂度 $O(N \times M)$。
• 优化点：能否预处理 nums2，一次性算出 nums2 中所有元素的“下一个更大元素”？

第二步：图形化模拟 (单调栈推演)

好的，同学。既然代码你已经熟悉了，我们现在抛开复杂的语法，用最形象的方式把这道题的逻辑“刻”在脑子里。

在 NOI 竞赛中，这种思路被称为**“找大哥”模型**。

---

第一步：生活化类比——“排队找大哥”

想象 nums2 是一排正在排队的人，每个数字代表一个人的身高。

规则如下：

1. 每个人都想在右边找到第一个比自己高的人（也就是他的“大哥”）。
2. 如果找到了，这个“大哥”的身高就是他的答案。
3. 如果直到队尾都没找到，他的答案就是 -1。

---

第二步：启发式模拟（请在草稿纸上跟我画图）

我们拿 nums2 = [2, 1, 5, 3, 4] 来举例。

请你在纸上画一个“暂候室”（这是一个栈，待找大哥的集合，并且因为后面元素入栈前和栈顶元素比较过才决定是否进栈，所以栈内具有单调性,只递增或递减），所有还没找到大哥的人，都要去那里等。

1. 2号入场：

   • 暂候室是空的，2号没看到大哥。
   • 动作：2号进入暂候室蹲着。
   • 纸上状态：暂候室 [2]（底→顶）

2. 1号入场：

   • 1号看了一眼暂候室最顶上的2号。
   • 1号（身高1）比2号（身高2）矮，1号没法当2号的大哥。
   • 动作：1号也进入暂候室，蹲在2号肩膀上。
   • 纸上状态：暂候室 [2, 1]

3. 5号入场（关键时刻！）：

   • 5号看了一眼暂候室顶上的1号。
   • 5号（身高5）比1号高！
   • 动作：1号开心地跳出来，记录：1的大哥是5。（可以用哈希表map或者数组array/vector来记）
   • 5号接着看现在顶上的2号。
   • 5号也比2号高！
   • 动作：2号也跳出来，记录：2的大哥是5。
   • 暂候室空了，5号进去蹲着。(5还没找到大哥）
   • 纸上状态：暂候室 [5]

4. 3号入场：

   • 3号比5号矮。
   • 动作：3号进入暂候室，蹲在5号肩膀上。
   • 纸上状态：暂候室 [5, 3]

5. 4号入场：

   • 4号比顶上的3号高。
   • 动作：3号跳出来，记录：3的大哥是4。
   • 4号看下一位（5号），4号比5号矮。
   • 动作：4号进入暂候室，蹲在5号肩膀上。
   • 纸上状态：暂候室 [5, 4]

最后扫尾： 队排完了，5号和4号还在暂候室里。说明他们右边没大哥了。 记录：5的大哥是-1，4的大哥是-1。

---

第三步：为什么这叫“单调栈”？

你观察一下刚才草稿纸上的暂候室：

• 里面的人从底到顶，身高是不是一定是从高到矮排队的？（比如 [5, 3]，[5, 4]）
• 逻辑推理：因为只要来了一个高个子，他就会把里面比他矮的人全部“踢”走（并成为他们的大哥）。
• 所以，暂候室里的元素永远保持单调性。这就是单调栈。

---

第四步：时间与空间复杂度分析

在 NOI 比赛中，我们要学会“数次数”：

• 时间复杂度：

  • 虽然代码里有 for 循环嵌套 while 循环，看起来像 $O(M^2)$？
  • 其实不然！你看，每一个人（数字）最多只会进暂候室一次，也最多出暂候室一次。
  • 如果有 $M$ 个数字，总动作次数就是 $2M$。
  • 所以复杂度是 $O(M)$，这在竞赛中是非常优秀的线性复杂度！

• 空间复杂度：

  • 最坏情况下（比如身高是递减的），所有人都会挤在暂候室里。
  • 所以我们需要一个大小为 $M$ 的栈，复杂度是 $O(M)$。

---

第五步：读题时的关键词总结

在 NOI 题目中，如果你看到以下表达，基本就是暗示你用这种“找大哥”模型：

1. “找右边第一个比它大的...” —— 典型的单调栈。
2. “找左边第一个比它小的...” —— 也是单调栈（只不过是从左往右扫，或者找比自己小的）。
3. “视野距离”/“能看到多少人” —— 每个人在遇到比自己高的人之前，中间有多少人。
4. “柱状图中最大的矩形” —— 左右边界的延伸就是找第一个比自己矮的。

---

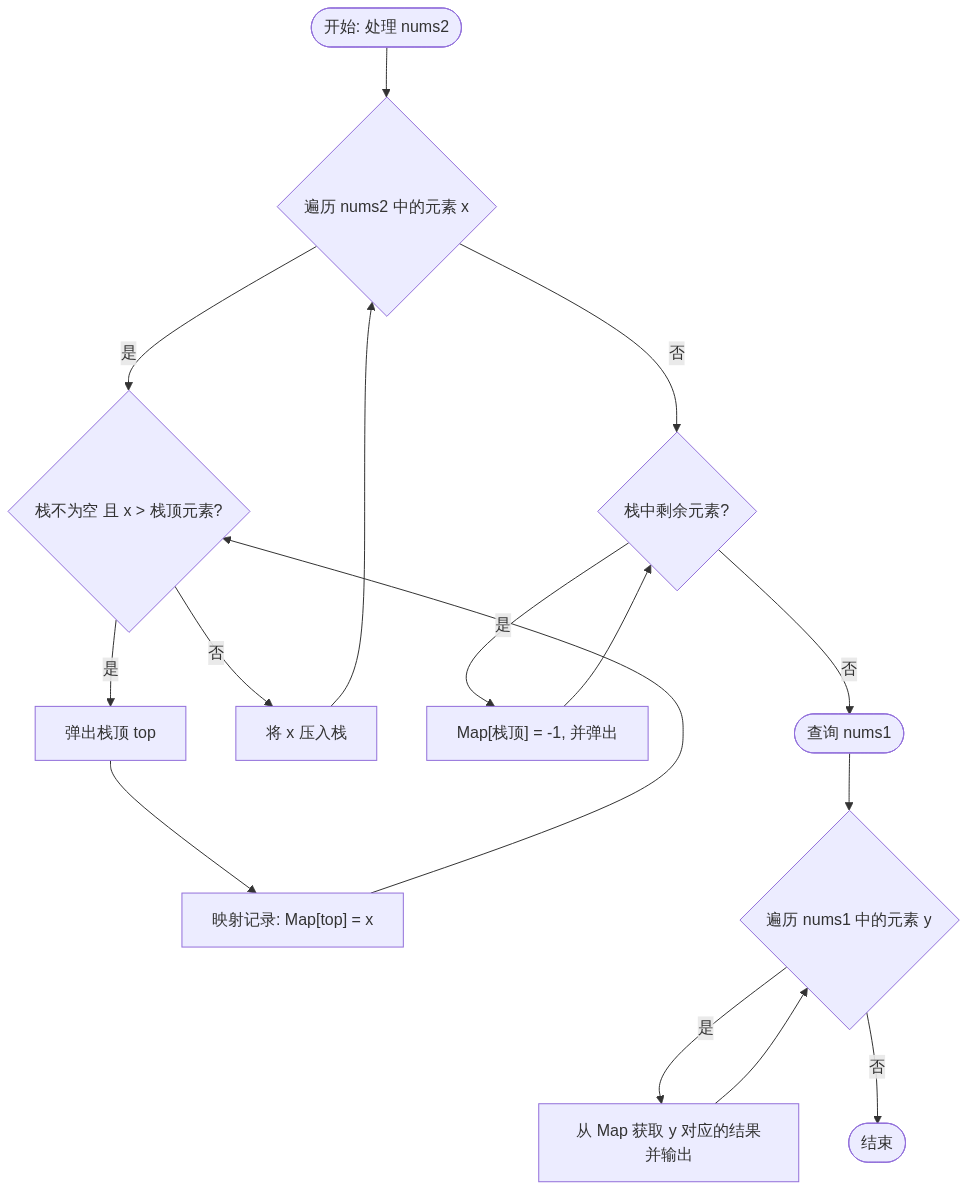
四、 算法流程图

在 NOI 编程中，我们通常使用 std::stack 和 std::unordered_map。

graph TD
    A(["开始: 处理 nums2"]) --> B{"遍历 nums2 中的元素 x"}
    B -- "是" --> C{"栈不为空 且 x > 栈顶元素?"}
    C -- "是" --> D["弹出栈顶 top"]
    D --> E["映射记录: Map[top] = x"]
    E --> C
    C -- "否" --> F["将 x 压入栈"]
    F --> B
    B -- "否" --> G{"栈中剩余元素?"}
    G -- "是" --> H["Map[栈顶] = -1, 并弹出"]
    H --> G
    G -- "否" --> I(["查询 nums1"])
    I --> J{"遍历 nums1 中的元素 y"}
    J -- "是" --> K["从 Map 获取 y 对应的结果并输出"]
    K --> J
    J -- "否" --> L(["结束"])

---

五、 读题关键词总结 (如何识别这类题？)

在做 OI 题目时，看到以下关键词，要立刻联想到单调栈：

1. “右侧第一个比当前值大/小”：这是单调栈的最典型特征。
2. “子集且不重复”：暗示了你可以通过哈希表或数组下标（如果值域小的话）建立唯一映射。
3. “相对顺序”：如果题目要求在原序列中找关系，通常涉及线性扫描。
4. “$O(N+M)$ 限制”：当 $N, M$ 达到 $10^5$ 级别时，暴力 $O(NM)$ 会超时，必须考虑单调栈。

---

六、 优化建议 (针对 NOI 实际比赛)

1. 值域优化：如果题目中 $nums2[i]$ 的范围很小（比如 $0 \sim 10^5$），在 NOI 比赛中，使用 int mp[100005] 数组代替 unordered_map 速度会更快，且能避免哈希冲突带来的常数开销。
2. 栈的实现：可以使用 int stk[MAXN], top = 0; 手写栈，比 std::stack 更快且方便调试。

在 NOI 读题时，看到以下组合描述，请立即联想“单调栈”：

1. “第一个比...大” (First Greater)。
2. “在右侧/左侧” (On the right/left side)。
3. “不含重复元素”：暗示可以用数值作为哈希表的 Key。
4. “$O(n)$ 时间要求”：这是单调栈与暴力 $O(n^2)$ 的核心区别。

教练点评： 单调栈是“空间换时间”和“延时处理”思想的结晶。本题通过栈暂时“存住”还没找到答案的数，等到“强者”出现时一并处理。掌握了这个模型，你就掌握了处理所有区间最值边界问题的金钥匙。加油！