你好，同学。今天我们进入“单调栈”专题的进阶篇——柱状图中最大的矩形。在 NOI 竞赛中，这道题是解决“极大化矩形”问题的基石，它不仅考察单调栈的熟练度，还考察了“边界哨兵”以及“空间延展”的几何思想。

【题目描述】柱状图中最大的矩形 (Largest Rectangle in Histogram)

题目背景： 在工业设计和图像处理中，常需要从离散的采样数据中寻找面积最大的矩形区域。现给定一组高度数据，请计算其形成的直方图中能勾勒出的最大矩形面积。

问题描述： 给定 $n$ 个非负整数，用来表示柱状图中各个柱子的高度。每个柱子彼此相邻，且宽度为 1。 求在该柱状图中，能够勾勒出来的矩形的最大面积。

输入格式： 第一行包含一个整数 $n$。 第二行包含 $n$ 个非负整数 $h_i$，表示每个柱子的高度。

输出格式： 输出一个整数，表示最大矩形的面积。

样例输入：

6
2 1 5 6 2 3

样例输出：

10

(解释：最大矩形由高度为 5 和 6 的两个柱子组成，面积为 5 * 2 = 10)

数据范围： 对于 $100\%$ 的数据：$1 \le n \le 10^5$，$0 \le h_i \le 10^4$。 注意：结果可能达到 $10^9$，建议使用 long long 以防万一，但在本题范围内 int 勉强可存。 内存限制：256MB，时间限制：1s。

一、 预备知识点

1. 单调栈 (Monotonic Stack)：本题的核心工具，用于在 $O(1)$ 时间内找到左右两侧第一个比当前高度矮的柱子。
2. 极大化思想：对于每一根柱子 $i$，如果我们以它的高度 $h_i$ 作为矩形的高，那么矩形能达到的最大宽度是由其左右两侧“第一个矮于自己的柱子”决定的。
3. 哨兵节点 (Sentinel)：通过在原数据首尾添加高度为 0 的柱子，简化边界判断逻辑。

二、 启发式教学：草稿纸上的推演

1. 核心直觉：以“我”为准

请在草稿纸上画出样例中的柱子。任选一根柱子（比如高度为 5 的那一根），思考：

• 如果我们要以这个高度 5 作为一个矩形的高度，这个矩形最左能伸展到哪？最右能伸展到哪？
• 结论：伸展到碰到“第一个比 5 矮”的柱子为止。

2. 单调栈的引入

我们需要快速找到左边第一个矮的（$L_i$）和右边第一个矮的（$R_i$）。

• 当我们从左向右遍历时，如果当前柱子 $h_i$ 比栈顶柱子高，说明栈顶的“右边界”还没到，把它压入栈。
• 如果当前柱子 $h_i$ 比栈顶柱子矮，那么栈顶柱子的右边界就找到了（就是当前位置 $i$）。
• 同时，栈顶柱子的左边界其实就是它在栈中的前一个元素。

3. 哨兵的妙用

在草稿纸上模拟时，你会发现：如果数据是单调递增的（如 1 2 3），栈会一直压入，最后怎么结算？

• 技巧：在数组末尾加一个高度为 0 的柱子，它会强制弹出栈内所有剩余的柱子并触发面积结算。

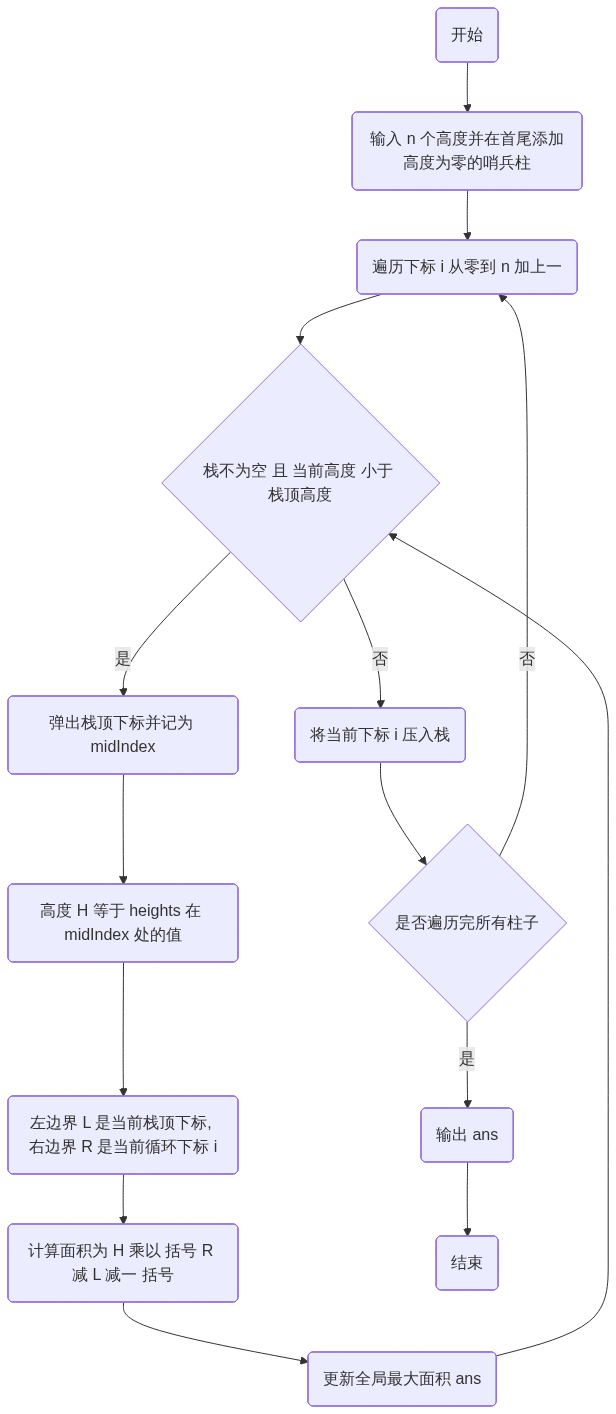
三、 算法流程图 (C++14 伪代码思路)

graph TD
    Start(开始) --> Init(输入 n 个高度并在首尾添加高度为零的哨兵柱)
    Init --> Loop(遍历下标 i 从零到 n 加上一)
    Loop --> WhileCond{栈不为空 且 当前高度 小于 栈顶高度}
    WhileCond -- 是 --> PopIdx(弹出栈顶下标并记为 midIndex)
    PopIdx --> CalcH(高度 H 等于 heights 在 midIndex 处的值)
    CalcH --> CalcW(左边界 L 是当前栈顶下标, 右边界 R 是当前循环下标 i)
    CalcW --> Area(计算面积为 H 乘以 括号 R 减 L 减一 括号)
    Area --> UpdateMax(更新全局最大面积 ans)
    UpdateMax --> WhileCond
    WhileCond -- 否 --> Push(将当前下标 i 压入栈)
    Push --> CheckEnd{是否遍历完所有柱子}
    CheckEnd -- 否 --> Loop
    CheckEnd -- 是 --> Output(输出 ans)
    Output --> End(结束)

四、 复杂度分析思考过程

• 时间复杂度：虽然有一个 while 嵌套在 for 中，但请注意，每个柱子的下标依然是入栈一次、出栈一次。因此总时间复杂度是确定的 $O(n)$。这在 $10^5$ 的规模下非常稳健。
• 空间复杂度：我们需要一个 $O(n)$ 的栈来存储下标，以及一个 $O(n)$ 的数组存高度。总空间 $O(n)$，完全符合 256MB 的限制。

五、 读题关键词总结 (题眼)

在 NOI 读题时，看到以下特征应联想到此题模型：

1. “最大矩形面积”：经典的单调栈或悬线法（Line Shaking Method）信号。
2. “连续的柱子”：暗示了宽度是可以累加的，而高度受限于区间内的最小值。
3. “第一个比...小”：只要逻辑中涉及寻找两侧的临界值，单调栈就是最优选。
4. $N$ 的量级：$10^5$ 的 $O(n)$ 解法通常是满分目标。

教练寄语： 这道题的难点在于计算宽度时 i - left - 1 的边界处理。通过加入左右哨兵（高度为 0），你可以省去繁琐的 stack.empty() 判断，让代码既简洁又优雅。在草稿纸上多画两遍栈的进出过程，你会发现单调栈其实就是在维护一个“待结算的阶梯”。加油！