钥匙和房间 (Keys and Rooms)

1. 题目描述

题目背景： 在图论算法中，判定图的连通性是核心考点之一。本题模拟了一个典型的有向图遍历场景：每个房间是一个节点，房间里的钥匙是通往其他节点的有向边。你需要判定从起点出发是否能到达所有节点。

任务描述： 有 $n$ 个房间，题目按从 $0$ 到 $n-1$ 编号。最初，你站在 $0$ 号房间内，该房间是解锁的。 每个房间里放有一批钥匙，每把钥匙上写着一个编号，代表你可以打开对应编号的房间。你可以自由地在已解锁的房间之间往返。 给定所有房间的钥匙列表，判定你是否能进入所有房间。

输入格式：

1. 第一行包含一个整数 $n$（$2 \le n \le 1000$），表示房间总数。
2. 接下来的 $n$ 行，第 $i$ 行（从 0 开始计数）描述第 $i$ 个房间的钥匙情况：
   • 每行开头是一个整数 $k_i$（$0 \le k_i \le 1000$），表示该房间内的钥匙数量。
   • 随后是 $k_i$ 个整数，表示钥匙能打开的房间编号。
3. 钥匙总数不超过 3000。

输出格式： 如果能进入所有房间，输出 true，否则输出 false。

样例 1： 输入：

4
1 1
1 2
1 3
0

输出：

true

(解释：从 0 号房开始，拿到进入 1 号房的钥匙；进入 1 号房拿到 2 号房的钥匙；进入 2 号房拿到 3 号房的钥匙。最终所有房都进去了。)

样例 2： 输入：

4
2 1 3
3 3 0 1
1 2
1 0

输出：

false

(解释：我们不能进入 2 号房间，因为唯一的钥匙在 2 号房自己手里。)

2. 预备知识点

1. 图的存储：邻接表（Adjacency List）。由于房间钥匙数量不一，使用 std::vector<int> adj[MAXN] 或链式前向星。
2. 图的遍历：
   • 深度优先搜索 (DFS)：利用递归或栈，一路走到底。
   • 广度优先搜索 (BFS)：利用队列，层层扩散。
3. 连通性判定：通过 visited 标记数组记录走过的路径。
4. 统计逻辑：遍历结束后，检查标记数组中 true 的个数是否等于 $n$。

3. 启发式思维引导

第一步：模型抽象

将房间看作“顶点”，钥匙看作从 A 房指向 B 房的“有向边”。

• 思考：这道题本质上在问什么？
• 结论：在一个有向图中，从节点 0 出发，所能到达的节点集合是否等于全集。

第二步：确定搜索策略

• 方案 A (DFS)：像走迷宫一样，拿到一把新钥匙就立刻去那个新房间，如果那个房间已经去过了，就退回。
• 方案 B (BFS)：手里拿个包，把 0 号房所有钥匙装进去，然后挨个去开，开完后把新房的钥匙也装进包里，直到包里的钥匙都用过。

第三步：草稿纸推演

1. 建立 vis 数组，初始全为 false。
2. 从房间 0 开始：vis(0) = true。
3. 遍历房间 0 的所有钥匙：
   • 如果是没去过的房 $K$，标记 vis(K) = true。
   • 进入房间 $K$ 继续此过程。
4. 最后数一数 vis 里有多少个 true。

第四步：复杂度分析

• 时间复杂度：$O(n + e)$，其中 $n$ 是房间数，$e$ 是钥匙总数。每个房间和每把钥匙只处理一次。
• 空间复杂度：$O(n)$，用于存储标记数组和递归栈（或队列）。

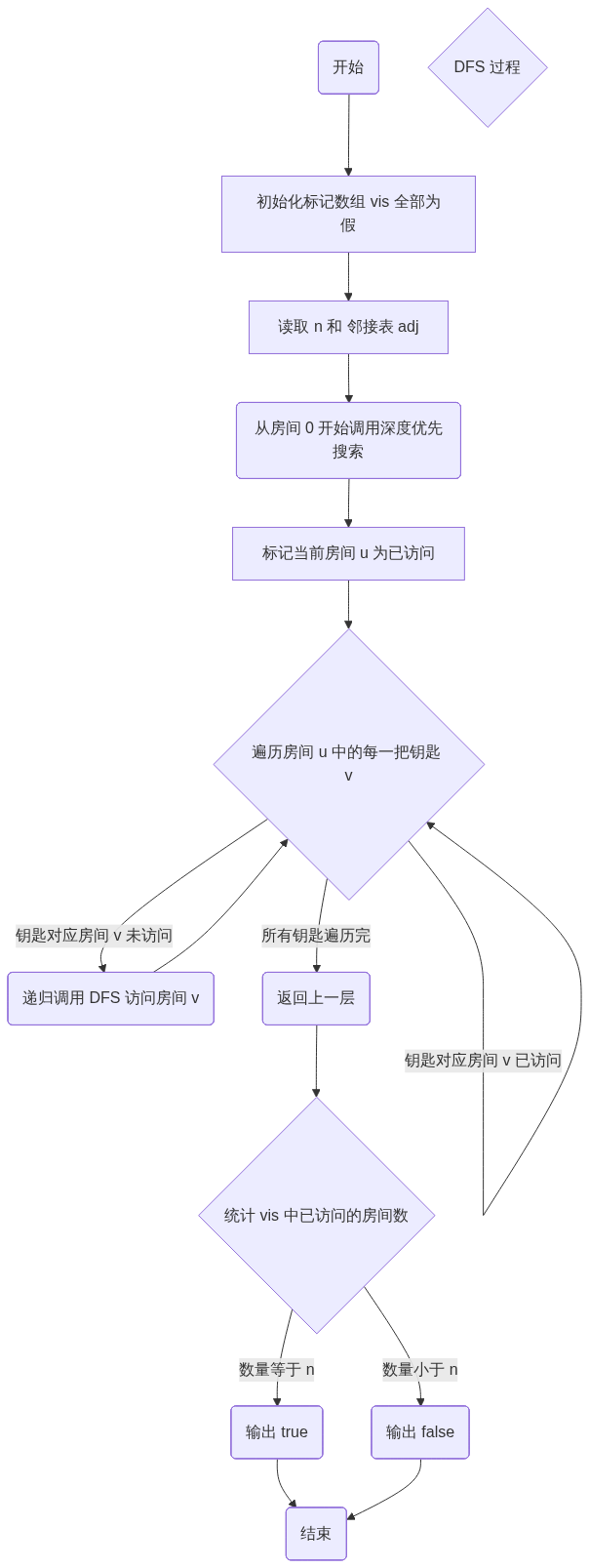
4. 算法流程图 (DFS 逻辑思路)

为遵循 Mermaid 语法并避免解析错误，特殊符号已替换为文字描述。

graph TD
    Start(开始) --> Init[初始化标记数组 vis 全部为假]
    Init --> Read[读取 n 和 邻接表 adj]
    Read --> CallDFS(从房间 0 开始调用深度优先搜索)
    
    SubGraph_DFS{DFS 过程}
    CallDFS --> Mark[标记当前房间 u 为已访问]
    Mark --> LoopKeys{遍历房间 u 中的每一把钥匙 v}
    LoopKeys -- 钥匙对应房间 v 未访问 --> CallDFS_V(递归调用 DFS 访问房间 v)
    CallDFS_V --> LoopKeys
    LoopKeys -- 钥匙对应房间 v 已访问 --> LoopKeys
    LoopKeys -- 所有钥匙遍历完 --> Return(返回上一层)
    
    Return --> Check{统计 vis 中已访问的房间数}
    Check -- 数量等于 n --> OutputTrue(输出 true)
    Check -- 数量小于 n --> OutputFalse(输出 false)
    OutputTrue --> End(结束)
    OutputFalse --> End

5. 读题关键词总结

在 NOI 竞赛中，通过关键词定位算法模型：

1. “进入所有房间” / “遍历所有”：
   • 直觉指示：图的遍历问题。判定是否存在一个源点能覆盖所有顶点。
2. “钥匙” / “持有关系”：
   • 直觉指示：典型的边权关系。通常是 有向图，因为 A 房有 B 房钥匙，不代表 B 房有 A 房钥匙。
3. “最初在 0 号房间”：
   • 直觉指示：指定了遍历的 源点。
4. $N \le 1000$：
   • 分析：数据量较小。$O(n^2)$ 的算法也能过，但图遍历 $O(n+e)$ 是最优解。注意，如果 $n$ 达到 $10^5$，必须使用高效的输入输出和链式前向星。

教练提示：在考场上，注意处理空房间的情况（没有钥匙）。DFS 的递归深度为 $n$，对于 $n=1000$ 来说完全安全。如果是 BFS，记得弹出队列时再处理逻辑，入队时标记访问以防止重复入队。加油！