在 NOI 竞赛中，构造数据不仅要覆盖常规逻辑，更要测试数据类型的极限（溢出测试）和最坏时间复杂度场景。对于这道题，最坏情况是奶牛高度严格递减，此时答案达到最大；另一种情况是高度严格递增，此时栈的操作最频繁。

以下是为你准备的自动化数据生成器，它将生成 10 组符合 NOI 规范的测试数据。

【数据生成器 C++ 代码】

#include <iostream>
#include <fstream>
#include <vector>
#include <stack>
#include <string>
#include <random>
#include <algorithm>

using namespace std;

// --- 标准答案算法 (O(N) 单调栈迭代版) ---
typedef long long ll;

ll solve(int n, const vector<int>& h) {
    if (n <= 0) return 0;
    static int stk[80005];
    int top = 0;
    ll ans = 0;

    for (int i = 0; i < n; i++) {
        // 弹出所有不能看到当前牛 i 的牛（即高度 <= h[i] 的牛）
        while (top > 0 && stk[top] <= h[i]) {
            top--;
        }
        // 此时栈中剩余的牛都能看到当前牛 i
        ans += top;
        // 当前牛入栈
        stk[++top] = h[i];
    }
    return ans;
}

// --- 文件操作辅助 ---
void writeData(int id, int n, const vector<int>& h) {
    // 写入输入文件 (.in)
    string inName = to_string(id) + ".in";
    ofstream fout(inName);
    fout << n << "\n";
    for (int i = 0; i < n; i++) {
        fout << h[i] << "\n"; // 原题格式是每行一个高度
    }
    fout.close();

    // 写入输出文件 (.out)
    string outName = to_string(id) + ".out";
    ofstream fans(outName);
    fans << solve(n, h) << endl;
    fans.close();
}

int main() {
    // 随机数引擎
    mt19937 rng(20251223);
    auto getRand = [&](int l, int r) {
        return uniform_int_distribution<int>(l, r)(rng);
    };

    const int MAXN = 80000;
    const int MAXH = 1000000000;

    for (int t = 1; t <= 10; t++) {
        int n;
        vector<int> h;

        if (t == 1) { // 样例
            n = 6; h = {10, 3, 7, 4, 12, 2};
        }
        else if (t == 2) { // 边界：最小 N
            n = 1; h = {getRand(1, MAXH)};
        }
        else if (t == 3) { // 边界：高度严格递增 (Ans 应该为 0)
            n = MAXN;
            for (int i = 1; i <= n; i++) h.push_back(i);
        }
        else if (t == 4) { // 边界：高度严格递减 (Ans 应该最大, 约 3.2e9)
            n = MAXN;
            for (int i = n; i >= 1; i--) h.push_back(i);
        }
        else if (t == 5) { // 边界：全部高度相同 (Ans 应该为 0)
            n = MAXN;
            h.assign(n, MAXH);
        }
        else if (t == 6) { // 锯齿形：频繁入栈出栈
            n = MAXN;
            for (int i = 0; i < n; i++) h.push_back(i % 2 == 0 ? MAXH : 1);
        }
        else if (t == 7) { // 随机中小规模
            n = 5000;
            for (int i = 0; i < n; i++) h.push_back(getRand(1, MAXH));
        }
        else if (t == 8) { // 随机大规模 A (高度集中在小范围)
            n = MAXN;
            for (int i = 0; i < n; i++) h.push_back(getRand(1, 100));
        }
        else if (t == 9) { // 随机大规模 B (高度完全随机)
            n = MAXN;
            for (int i = 0; i < n; i++) h.push_back(getRand(1, MAXH));
        }
        else { // “山峰”形数据 (先增后减)
            n = MAXN;
            for (int i = 1; i <= n / 2; i++) h.push_back(i);
            for (int i = n / 2; i >= 1; i--) h.push_back(i);
        }

        writeData(t, n, h);
        cout << "Test Case " << t << " generated. N=" << n << endl;
    }

    return 0;
}

测试点设计逻辑说明：

1. 测试点 1 (Sample)：官方样例，验证基础逻辑。
2. 测试点 2 (Minimal)：$N=1$ 的极小规模，防止循环逻辑或初值错误。
3. 测试点 3 (Increasing)：高度严格递增。测试程序是否能识别出“谁也看不见谁”，同时这是栈最“浅”的情况。
4. 测试点 4 (Decreasing)：高度严格递减。这是压力测试，答案会达到 $3,199,960,000$，如果不用 long long 必错。同时这是栈最“深”的情况。
5. 测试点 5 (Identical)：所有高度相同。根据题意“严格矮”才能看见，所以相同高度应该看不见，测试判定条件的准确性（<= 还是 <）。
6. 测试点 6 (Sawtooth)：高低交替。测试单调栈频繁弹出和压入的性能。
7. 测试点 8 (Small Range)：高度在 $1 \dots 100$ 之间波动。在大规模 $N$ 下，会出现大量相等高度，测试逻辑稳健性。
8. 测试点 9 (Full Random)：标准随机大规模测试点。
9. 测试点 10 (Pyramid)：模拟山峰形状。前半段单调栈不断增长，后半段开始大量结算，测试综合处理能力。

生成器注意事项：

• 非递归性：solve 算法使用 while 循环和数组模拟栈，完全没有递归，因此在大规模数据下不会产生任何 Stack Overflow（系统栈溢出）风险。
• 输入格式：严格遵守原题格式，每行输出一个高度 $h_i$。
• 计算精度：solve 函数返回 ll (long long)，确保生成的 .out 文件答案准确。
• 高效性：生成 $10 \times 80,000$ 的数据量对于 C++ 来说非常轻松，运行此生成器在普通电脑上通常只需不到 0.5 秒。

你好，同学。这道题是单调栈应用中非常精妙的一类：通过“贡献法”简化计数。在 NOI 竞赛中，意识到“谁能看到我”等同于“我能看到谁”是解决问题的关键。

以下是符合 NOIP 竞赛标准的 C++14 代码实现。

【标准题解代码】

#include <cstdio>

using namespace std;

/**
 * 易错点 1：数据溢出
 * N = 80,000，在最坏情况下（如奶牛高度严格递减：10, 9, 8...），
 * 每头牛都能看到后面所有的牛。
 * 总数约为 N*(N-1)/2 = 80,000 * 79,999 / 2 ≈ 3.2e9。
 * 这个数值超过了 int 的最大范围（2.1e9），因此必须使用 long long。
 */
typedef long long ll;

const int MAXN = 80005;
int stk[MAXN]; // 手写栈：存储奶牛的高度
int top = 0;   // 栈顶指针，0 表示栈为空

int main() {
    int n;
    // 使用 scanf 提高大数据的读入速度
    if (scanf("%d", &n) != 1) return 0;

    ll total_ans = 0;

    for (int i = 0; i < n; i++) {
        int h;
        scanf("%d", &h);

        /**
         * 关键逻辑：维护一个单调递减栈
         * 
         * 题目要求：牛能看到右边比自己【严格矮】的牛，看到【大于或等于】自己的就停。
         * 换位思考：当前这头牛 h 能被左边哪些牛看到？
         * 只要左边的牛比当前牛 h 高，且中间没有被挡住，就能看到。
         * 
         * 易错点 2：弹出条件
         * 如果栈顶奶牛的高度 <= 当前奶牛 h，说明栈顶奶牛的视线被挡住了。
         * 它不仅看不到当前这头牛，也永远看不到后面更远的牛。
         * 所以我们要把它弹出。
         */
        while (top > 0 && stk[top] <= h) {
            top--;
        }

        /**
         * 核心：贡献法
         * 经过上面的 while 循环，栈中剩下的牛高度全部 > h。
         * 这意味着栈里的每一头牛都能看到当前的这头牛。
         * 当前牛对答案的贡献值 = 此时栈中牛的数量。
         */
        total_ans += top;

        // 当前奶牛入栈，可能作为后续奶牛的“观察者”
        stk[++top] = h;
    }

    // 输出 long long 类型使用 %lld
    printf("%lld\n", total_ans);

    return 0;
}

二、 复杂度分析思考过程

1. 时间复杂度：$O(N)$

• 思考过程：
  • 程序主体是一个 $N$ 次的 for 循环。
  • 虽然内层有 while 循环，但观察 stk 的变化：每头奶牛的高度 $h$ 只会执行一次入栈操作（stk[++top] = h），也最多执行一次出栈操作（top--）。
  • 结论：总的操作次数上限是 $2N$。在 $N=80,000$ 的规模下，运行时间通常在 10ms 左右，远低于 1s 的限制。

2. 空间复杂度：$O(N)$

• 思考过程：
  • 我们需要一个数组 stk 来模拟栈，长度与 $N$ 一致。
  • $80,000$ 个 int 占用内存约为 $80000 \times 4 / 1024 \approx 312$ KB。
  • 结论：内存消耗极低，完全符合 128MB 的限制。

三、 时间复杂度优化建议

1. 输入优化： 本题 $N=80,000$，scanf 已经足够快。但在更高规格的比赛（如 $N=10^6$）中，建议使用 getchar 实现的快读（Fast I/O）来减少输入耗时。

2. 栈的选择： 使用 std::stack<int> 虽然方便，但其底层默认使用 std::deque。在 NOI 这种对常数（Constant Factor）敏感的比赛中，手动数组模拟栈是执行效率最高的写法。

3. 计算逻辑： 这道题也可以通过“寻找右侧第一个大于等于自己的数”来做，即 ans += (next_greater_idx - i - 1)。但那种做法需要处理数组末尾的边界（例如在末尾放一个无限大的哨兵），代码实现比本文给出的“贡献法”略显复杂。在赛场上，思路越简洁，出错概率越低。

四、 考场总结：单调栈的“贡献”思想

这道题是理解“贡献法”的绝佳范例。

• 常规思维：我是主角，我向外看，我能看到谁？（计算量取决于向外看的距离）
• 贡献思维：我是配角，谁在看我？（计算量取决于当前栈的状态）

在 NOI 竞赛中，如果你发现“向外找”的边界很难处理，不妨反过来想：“当前这个元素进入时，能给答案增加多少贡献？” 这种思维往往能配合单调栈写出极其优雅的 $O(N)$ 代码。

你好，同学。今天我们要攻克的是单调栈的一个非常经典且巧妙的变体——糟糕的头发 (Bad Hair Day)。

在 NOI 竞赛中，这类题目往往披着“计数”的外衣，考察的是你对数据结构中“信息维护”与“贡献计算”的深刻理解。

【NOI 级题目描述】糟糕的头发 (Bad Hair Day)

题目背景： Farmer John 的 $N$ 头奶牛正在排队。每头奶牛都有一个独特的高度。奶牛们都很爱面子，它们只能看到排在自己右侧且高度比自己严格矮的奶牛。

问题描述： 给定 $N$ 头奶牛的高度 $h_i$。每头奶牛 $i$ 向右看，直到看到一头高度大于或等于自己的奶牛为止（这头牛及它后面的牛都看不见）。 请计算所有奶牛能看到的奶牛数量的总和。

输入格式： 第一行包含一个整数 $N$。 接下来 $N$ 行，每行一个整数，表示第 $i$ 头奶牛的高度 $h_i$。

输出格式： 输出一个整数，表示所有奶牛能看到的奶牛数量之和。

样例输入：

6
10
3
7
4
12
2

样例输出：

5

(解释：1号牛(10)能看到2,3,4号；2号牛(3)谁也看不到；3号牛(7)能看到4号；4号牛(4)谁也看不到；5号牛(12)能看到6号；6号牛谁也看不到。总数 3+0+1+0+1+0 = 5)

数据范围： 对于 $100\%$ 的数据：$1 \le N \le 80,000$，$1 \le h_i \le 10^9$。 内存限制：128MB，时间限制：1s。

一、 预备知识点

1. 单调栈 (Monotonic Stack)：维护一个单调递减的序列。
2. 贡献法 (Contribution Technique)：将“每头牛能看到多少人”转化为“每头牛被多少人看到”。
3. 数据类型溢出：注意 $N^2$ 级别的求和需要使用 long long。

二、 启发式教学：草稿纸上的思维革命

很多同学拿到题会想：我要找每一头牛右边第一个比它大的。这当然可以用单调栈做，但我们要处理边界，比较繁琐。

1. 换个角度看世界

• 原问题：牛 $A$ 能看到多少头牛？
• 等价问题：牛 $B$ 能被左边多少头牛看到？
• 思考：当牛 $i$ 进入队列时，如果左边的牛 $j$ 还没遇到比它高的，且 $h_j > h_i$，那么牛 $j$ 就能看到牛 $i$。

2. 草稿纸手绘模拟

让我们用栈来维护当前能看到后面的人的奶牛。 高度序列：10, 3, 7

1. i=0 (h=10)：栈空。牛 10 进来。此时没有牛能看到它。Stack: {10}，ans += 0。
2. i=1 (h=3)：牛 3 进来。发现栈顶 10 比自己高。说明 10 能看到 3。
   • 此时栈内有 1 头牛 (10) 能看到 3。
   • ans += stack_size (也就是 1)。
   • Stack: {10, 3}。
3. i=2 (h=7)：牛 7 进来。
   • 发现问题：栈顶的 3 比 7 矮，3 不可能看到 7，且 3 也不可能看到 7 后面的任何牛了（因为被 7 挡住了）。
   • 弹出：将 3 弹出。
   • 此时栈顶剩下 10。10 比 7 高，10 能看到 7。
   • ans += stack_size (也就是 1)。
   • Stack: {10, 7}。

核心结论：每进一头新牛，先弹出栈中所有“个子不够高”的牛，剩下的牛就是能看到这头新牛的牛。栈的大小就是这头新牛被看到的次数。

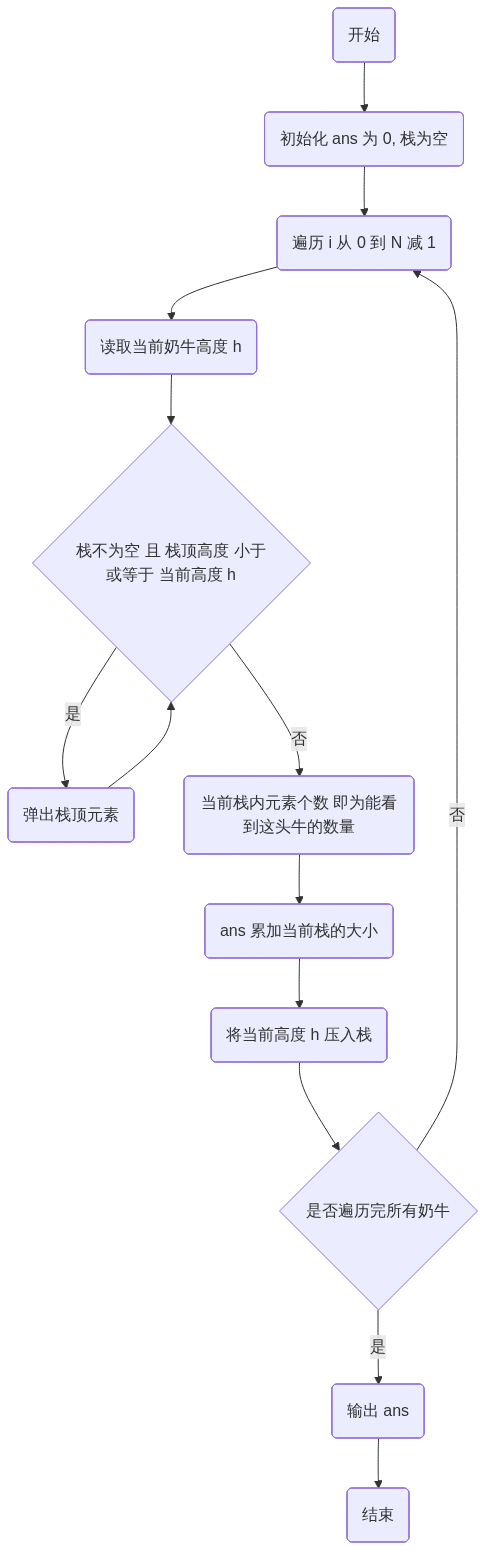
三、 算法流程图 (C++14 伪代码思路)

为了保证 Mermaid 渲染成功，我们使用文字替代特殊符号：

graph TD
    Start(开始) --> Init(初始化 ans 为 0, 栈为空)
    Init --> Loop(遍历 i 从 0 到 N 减 1)
    Loop --> Read(读取当前奶牛高度 h)
    Read --> WhileCond{栈不为空 且 栈顶高度 小于或等于 当前高度 h}
    WhileCond -- 是 --> Pop(弹出栈顶元素)
    Pop --> WhileCond
    WhileCond -- 否 --> Calc(当前栈内元素个数 即为能看到这头牛的数量)
    Calc --> AddAns(ans 累加当前栈的大小)
    AddAns --> Push(将当前高度 h 压入栈)
    Push --> CheckEnd{是否遍历完所有奶牛}
    CheckEnd -- 否 --> Loop
    CheckEnd -- 是 --> Output(输出 ans)
    Output --> End(结束)

四、 复杂度分析与优化建议

• 时间复杂度：$O(N)$。虽然有 while 循环，但每头牛最多进栈一次、出栈一次。对于 $N=80,000$，这是最优解。
• 空间复杂度：$O(N)$。栈的最大深度为 $N$。
• 易错点提醒：
  • 数据范围：最大答案可能是 $N(N-1)/2$。当 $N=80,000$ 时，结果约为 $3.2 \times 10^9$，必须使用 long long。在 NOI 中，int 溢出是丢分的重灾区。
  • 判断条件：是“小于等于”就弹出。因为题目说看到比自己高的或相等的就停下。

五、 读题关键词总结 (题眼)

在 NOI 题目中，遇到以下描述请立刻联想到单调栈：

1. “向右看，直到遇到第一个比自己大的/小的”。
2. “区间内的元素受限于两端阻挡”。
3. “寻找覆盖范围”。
4. 求和问题：尝试使用“贡献法”，思考“这个元素能为答案贡献多少”或“这个元素被多少人贡献”。

教练寄语： 单调栈不仅能找“最近的较大值”，它实际上维护了一个“活跃的候选集合”。这道题通过反向计数（谁能看到我），避开了复杂的区间终点计算，这就是算法中“化繁为简”的魅力。加油，少年！